Page 141 - Geosystems An Introduction to Physical Geography 4th Canadian Edition

Chapter 4 atmosphere and Surface Energy Balances 105
The surface in any given location receives and loses shortwave and longwave energy according to the follow- ing simple scheme:
+SWT – SWc + LWT – LWc = NET R (Insolation) (Reflection) (Infrared) (Infrared) (Net radiation)
We use SW for shortwave and LW for longwave for simplicity.*
Figure 4.13 shows the components of a surface en- ergy balance over a soil surface. The soil column contin- ues to a depth at which energy exchange with surround- ing materials or with the surface becomes negligible, usually less than a metre. Heat is transferred by conduc- tion through the soil, predominantly downward during the day (or in summer) and toward the surface at night (or in winter). Energy moving from the atmosphere into the surface is reported as a positive value (a gain), and energy moving outward from the surface, through sen- sible and latent heat transfers, is reported as a negative value (a loss) in the surface account.
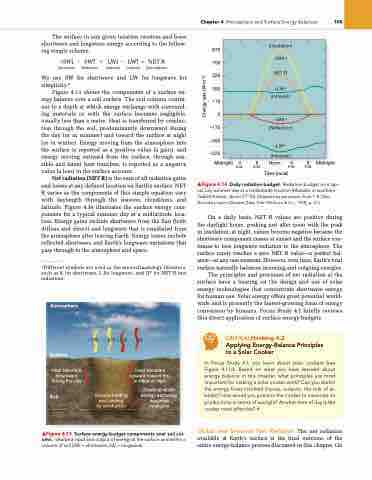
Net radiation (NET R) is the sum of all radiation gains and losses at any defined location on Earth’s surface. NET R varies as the components of this simple equation vary with daylength through the seasons, cloudiness, and latitude. Figure 4.14 illustrates the surface energy com- ponents for a typical summer day at a midlatitude loca- tion. Energy gains include shortwave from the Sun (both diffuse and direct) and longwave that is reradiated from the atmosphere after leaving Earth. Energy losses include reflected shortwave and Earth’s longwave emissions that pass through to the atmosphere and space.
*Different symbols are used in the microclimatology literature, such as K for shortwave, L for longwave, and Q* for NET R (net radiation).
▲Figure 4.13 Surface energy-budget components over soil col- umn. idealized input and output of energy at the surface and within a column of soil (SW = shortwave, lW = longwave).
875
700
525
350
175
0 –175 –350 –525
Midnight
4 8 A.M. A.M.
Noon Time (local)
(Insolation) +SW
NET R
+LW (Infrared)
–SW (Reflection)
–LW (Infrared)
▲Figure 4.14 Daily radiation budget. Radiation budget on a typi- cal July summer day at a midlatitude location (Matador in southern Saskatchewan, about 51° n). [adapted by permission from T. R. Oke, Boundary Layer Climates (new york: Methuen & Co., 1978), p. 21.]
On a daily basis, NET R values are positive during the daylight hours, peaking just after noon with the peak in insolation; at night, values become negative because the shortwave component ceases at sunset and the surface con- tinues to lose longwave radiation to the atmosphere. The surface rarely reaches a zero NET R value—a perfect bal- ance—at any one moment. However, over time, Earth’s total surface naturally balances incoming and outgoing energies.
The principles and processes of net radiation at the surface have a bearing on the design and use of solar energy technologies that concentrate shortwave energy for human use. Solar energy offers great potential world- wide and is presently the fastest-growing form of energy conversion by humans. Focus Study 4.1 briefly reviews this direct application of surface energy budgets.
4
P.M. P.M.
Midnight
8
Atmosphere
Surface
+ SW
– SW + LW
– LW
Heat transfers upward toward the surface at night
Depth at which energy exchange becomes negligible
Heat transfers downward during the day
Soil
Ground heating and cooling by conduction
CrITICAlthinking 4.2
Applying Energy-Balance Principles to a Solar Cooker
in Focus Study 4.1, you learn about solar cookers (see Figure 4.1.1c). Based on what you have learned about energy balance in this chapter, what principles are most important for making a solar cooker work? Can you sketch the energy flows involved (inputs, outputs, the role of al- bedo)? How would you position the cooker to maximize its productivity in terms of sunlight? at what time of day is the cooker most effective? •
Global and Seasonal net Radiation The net radiation available at Earth’s surface is the final outcome of the entire energy-balance process discussed in this chapter. On
Energy rate (W·m–2)