Page 825 - Introduction to Programming with Java: A Problem Solving Approach

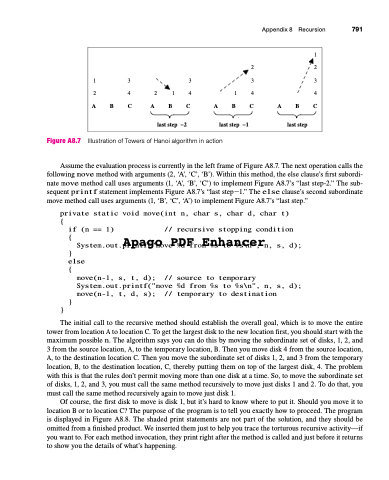
Figure A8.7 Illustration of Towers of Hanoi algorithm in action
Assume the evaluation process is currently in the left frame of Figure A8.7. The next operation calls the following move method with arguments (2, ‘A’, ‘C’, ‘B’). Within this method, the else clause’s first subordi- nate move method call uses arguments (1, ‘A’, ‘B’, ‘C’) to implement Figure A8.7’s “last step-2.” The sub- sequent printf statement implements Figure A8.7’s “last step􏰁1.” The else clause’s second subordinate move method call uses arguments (1, ‘B’, ‘C’, ‘A’) to implement Figure A8.7’s “last step.”
private static void move(int n, char s, char d, char t)
{
}
if (n == 1)
{
// recursive stopping condition
Apago PDF Enhancer
System.out.printf("move %d from %s to %s\n", n, s, d);
}
else
{
}
move(n-1, s, t, d); // source to temporary
System.out.printf("move %d from %s to %s\n", n, s, d);
move(n-1, t, d, s); // temporary to destination
The initial call to the recursive method should establish the overall goal, which is to move the entire tower from location A to location C. To get the largest disk to the new location first, you should start with the maximum possible n. The algorithm says you can do this by moving the subordinate set of disks, 1, 2, and 3 from the source location, A, to the temporary location, B. Then you move disk 4 from the source location, A, to the destination location C. Then you move the subordinate set of disks 1, 2, and 3 from the temporary location, B, to the destination location, C, thereby putting them on top of the largest disk, 4. The problem with this is that the rules don’t permit moving more than one disk at a time. So, to move the subordinate set of disks, 1, 2, and 3, you must call the same method recursively to move just disks 1 and 2. To do that, you must call the same method recursively again to move just disk 1.
Of course, the first disk to move is disk 1, but it’s hard to know where to put it. Should you move it to location B or to location C? The purpose of the program is to tell you exactly how to proceed. The program is displayed in Figure A8.8. The shaded print statements are not part of the solution, and they should be omitted from a finished product. We inserted them just to help you trace the torturous recursive activity—if you want to. For each method invocation, they print right after the method is called and just before it returns to show you the details of what’s happening.
Appendix 8 Recursion 791
1 22 13333 24214144 ABCABCABCABC
last step −2 last step −1 last step