Page 260 - Buku Paket Kelas 11 Matematika

Coba kamu amati proses matematis berikut. Misalkan x2 = x1 + Dx dan y2 = y1 + Dy, jika Dx semakin kecil maka Q akan bergerak mendekati P (Jika Dx → 0 maka Q → P).
Perhatikan kembali gambar!
y
y1
y2
P
P(x1,y1)
garis sekan garis sekan
garis sekan garis sekan
garis tangen/singgung
∆y
∆x
Q
Q(x2,y2)
y = f(x) x2x1 x
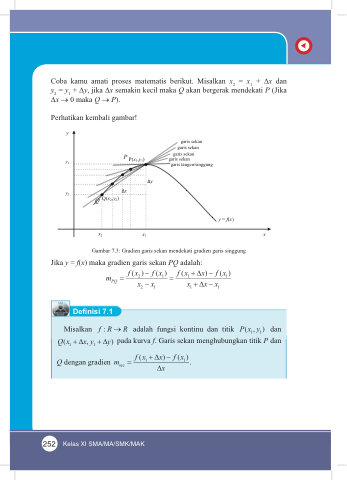
Gambar 7.3: Gradien garis sekan mendekati gradien garis singgung
Jika y = f(x) maka gradien garis sekan PQ adalah:
mPQ = f(x2)−f(x1)= f(x1+∆x)−f(x1)
x2 − x1 x1 + ∆x − x1
Definisi 7.1
Misalkan f : R → R adalah fungsi kontinu dan titik P(x1, y1) dan Q(x1 + ∆x, y1 + ∆y) pada kurva f. Garis sekan menghubungkan titik P dan
Q dengan gradien msec = f (x1 +∆x)− f (x1). ∆x
252 Kelas XI SMA/MA/SMK/MAK