Page 119 - Green - Maritime Archaeology: A Technical Handbook. 2nd ed

98 Maritime Archaeology: A Technical Handbook, Second Edition
Y
C (x3,y3)
a
cX 0 A (0,0) B (c,0)
222 Cos A = c + b — a
2bc
x3 = bCosA y3 = bSinA
b
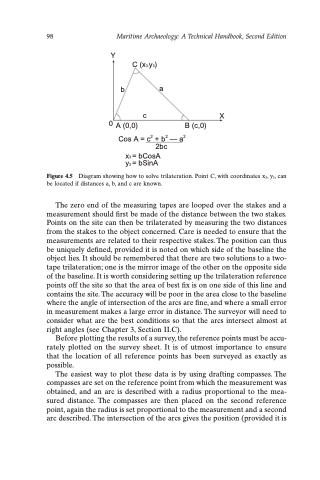
Figure 4.5 Diagram showing how to solve trilateration. Point C, with coordinates x3, y3, can be located if distances a, b, and c are known.
The zero end of the measuring tapes are looped over the stakes and a measurement should first be made of the distance between the two stakes. Points on the site can then be trilaterated by measuring the two distances from the stakes to the object concerned. Care is needed to ensure that the measurements are related to their respective stakes. The position can thus be uniquely defined, provided it is noted on which side of the baseline the object lies. It should be remembered that there are two solutions to a two- tape trilateration; one is the mirror image of the other on the opposite side of the baseline. It is worth considering setting up the trilateration reference points off the site so that the area of best fix is on one side of this line and contains the site. The accuracy will be poor in the area close to the baseline where the angle of intersection of the arcs are fine, and where a small error in measurement makes a large error in distance. The surveyor will need to consider what are the best conditions so that the arcs intersect almost at right angles (see Chapter 3, Section II.C).
Before plotting the results of a survey, the reference points must be accu- rately plotted on the survey sheet. It is of utmost importance to ensure that the location of all reference points has been surveyed as exactly as possible.
The easiest way to plot these data is by using drafting compasses. The compasses are set on the reference point from which the measurement was obtained, and an arc is described with a radius proportional to the mea- sured distance. The compasses are then placed on the second reference point, again the radius is set proportional to the measurement and a second arc described. The intersection of the arcs gives the position (provided it is