Page 135 - Algebra

x2 + 2x + 9
a = 1, b = 2, c = 9
𝑏 2𝑎
x = –1
Put f(-1) in x2 + 2x + 9 = (-1) + 9
=8
So, the point is (–1, 8)
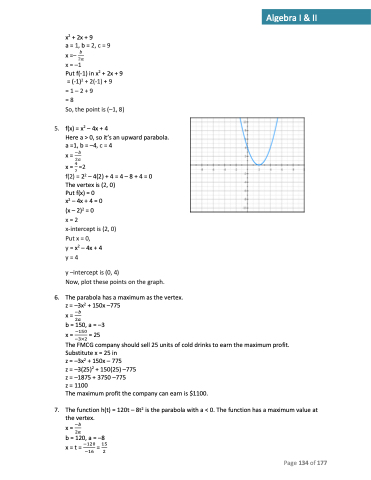
5. f(x) = x2 – 4x + 4
Here a > 0, so it’s an upward parabola.
x =–
=1–2+9
2 + 2(-1)
a =1, b = –4, c = 4 −𝑏
x = 2𝑎
x = 4 =2
2
f(2)=22 –4(2)+4=4–8+4=0 The vertex is (2, 0)
Put f(x) = 0
x2 – 4x + 4 = 0
(x–2)2 =0
x= 2
y = x2 – 4x + 4 y=4
6. The parabola has a maximum as the vertex.
z = –3x2 + 150x –775
−𝑏 x = 2𝑎
b = 150, a = –3
−150
−3×2
The FMCG company should sell 25 units of cold drinks to earn the maximum profit. Substitute x = 25 in
z=–3x2 +150x–775
z = –3(25)2 + 150(25) –775
z = –1875 + 3750 –775
z = 1100
The maximum profit the company can earn is $1100.
7. The function h(t) = 120t – 8t2 is the parabola with a < 0. The function has a maximum value at the vertex.
−𝑏 x = 2𝑎
b = 120, a = –8
x= t = =
x-intercept is (2, 0)
Put x = 0,
y –intercept is (0, 4)
Now, plot these points on the graph.
x =
= 25
−120 15
−16
2
Page 134 of 177
Algebra I & II