Page 220 - Buku Paket Kelas 12 Matematika

8QWXN PHPSHUND\D ZDZDVDQ GDQ SHQJHWDKXDQ $QGD􏰃 EHULNXW DNDQ GLVDMLNDQ VHEXDK FRQWRK SHPEXNWLDQ VHFDUD GHGXNWLI XQWXN PHPEXNWLNDQ NHVLPSXODQ􏰊 konjektur tentang kesebangunan dua segitiga jika diketahui rasio dari ukuran VHPXD VLVL \DQJ EHUVHVXDLDQ 􏰒Konjektur Kesebangunan Sisi-Sisi-Sisi).
Contoh Soal 4.2.2
%XNWL .RQMHNWXU .HVHEDQJXQDQ VHJLWLJD 6LVL􏰂6LVL􏰂6LVL
'LEHULNDQ GXD VHJLWLJD $%& GDQ '()􏰃 GL PDQD AB = AC = BC 􏰃 PDND
¨ABC ¨DEF. 3HPEXNWLDQ􏰆
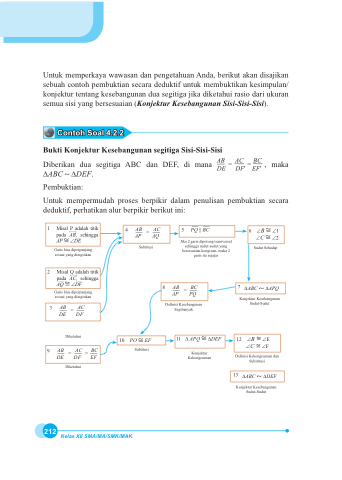
Untuk mempermudah proses berpikir dalam penulisan pembuktian secara GHGXNWLI􏰃 SHUKDWLNDQ DOXU EHUSLNLU EHULNXW LQL􏰆
DE DF' EF'
1 Misal P adalah titik
m􏰬o
pada AB􏰃 VHKLQJJD 􏰬􏰬 􏰬􏰬
4 AB = AC AP AQ
5 PQ || BC
6 􏰫B 􏰫1 􏰫C 􏰫2
AP 􏰫DE
*DULV ELVD GLSHUSDQMDQJ sesuai yang diinginkan
*DULV ELVD GLSHUSDQMDQJ sesuai yang diinginkan
Diketahui
Diketahui
212 Kelas XII SMA/MA/SMK/MAK
Subtitusi
Jika 2 garis dipotong transversal sehingga sudut-sudut yang EHUVHVXDLDQ NRQJUXHQ􏰃 PDND 􏰇 garis itu sejajar
'H¿QLVL .HVHEDQJXQDQ Segibanyak
Konjektur Kekongruenan
Sudut Sehadap
Konjektur Kesebangunan Sudut-Sudut
'H¿QLVL .HNRQJUXHQDQ GDQ Substitusi
Konjektur Kesebangunan Sudut-Sudut
2 Misal Q adalah titik
m􏰬o
pada AC􏰃 sehingga 􏰬􏰬 􏰬􏰬
AQ 􏰫DF
3 AB = AC DE DF
8 AB = BC AP PQ
7 ¨ABC ¨APQ
10 PO EF
􏰅􏰅 ¨APQ ¨DEF
12 􏰫B 􏰫E 􏰫C 􏰫F
􏰑 AB = AC = BC DE DF EF
Subtitusi
13 ¨ABC ¨DEF