Page 270 - MATHEMATICS COURSE FOR SECONDARY SCHOOLS BOOK 2

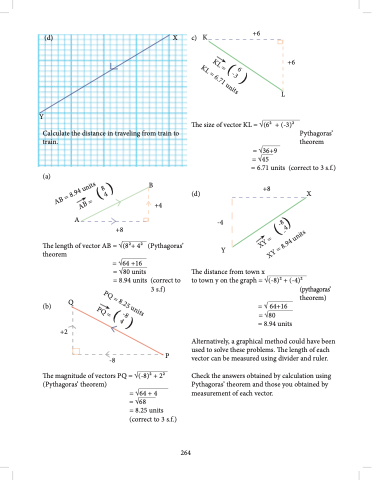
(d) X
c)K
+6
+6
L
Y
Calculate the distance in traveling from train to train.
The size of vector KL = √(62 + (-3)2
= √36+9 = √45
Pythagoras’ theorem
(a)
B +4
(Pythagoras’
= 6.71 units (correct to 3 s.f.) (d) +8 X
-4 Y
A
+8
The length of vector AB = √(82+ 42
theorem
= √64 +16
= √80 units
= 8.94 units (correct to
3 s.f)
(b)
Q
+2
-8
= √ 64+16 = √80
= 8.94 units
(pythagoras’ theorem)
The distance from town x
to town y on the graph = √(-8)2 + (-4)2
P
Alternatively, a graphical method could have been used to solve these problems. The length of each vector can be measured using divider and ruler.
Check the answers obtained by calculation using Pythagoras’ theorem and those you obtained by measurement of each vector.
The magnitude of vectors PQ = √(-8)2 + 22
(Pythagoras’ theorem)
= √64 + 4
= √68
= 8.25 units (correct to 3 s.f.)
264
KL = ( )
KL = 6.71 units
6 -3
AB =
(8 ) 4
AB = 8.94 units
XY =
(-8)
4 -
XY = 8.94 units
PQ = 8.25 units
PQ = ( )
-8 4