Page 293 - MATHEMATICS COURSE FOR SECONDARY SCHOOLS BOOK 2

COLLINEAR VECTORS AND RATIO
C
D
B
From the polygon above:
AE = AB + BC + CD + DE
(Anti-clockwise) (clockwise)
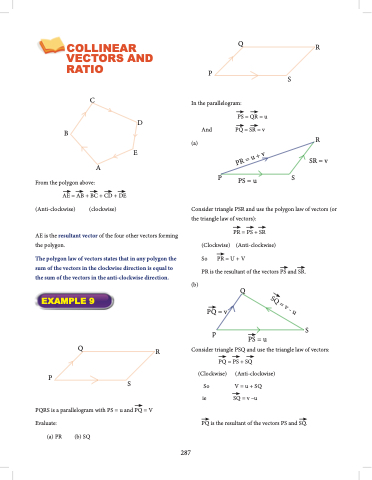
Q P
In the parallelogram:
PS = QR = u
R S
R SR = v
E A
AE is the resultant vector of the four other vectors forming the polygon.
The polygon law of vectors states that in any polygon the sum of the vectors in the clockwise direction is equal to the sum of the vectors in the anti-clockwise direction.
Consider triangle PSR and use the polygon law of vectors (or the triangle law of vectors):
PR = PS + SR (Clockwise) (Anti-clockwise)
So PR = U + V
PR is the resultant of the vectors PS and SR.
(b)
Q PQ = v
p
(a)
And
PQ = SR = v
P PS = u S
EXAMPLE 9
Q P
S PS = u
(a) PR (b) SQ
R
S
Consider triangle PSQ and use the triangle law of vectors: PQ = PS + SQ
287
(Clockwise) So
(Anti-clockwise)
PQRS is a parallelogram with PS = u and PQ = V Evaluate:
ie
PQ is the resultant of the vectors PS and SQ.
V = u + SQ SQ = v –u
PR = u + v
SQ = v - u