Page 91 - MATHEMATICS COURSE FOR SECONDARY SCHOOLS BOOK 2

AREA AND SEGMENT OF A CIRCLE
EXAMPLE 5
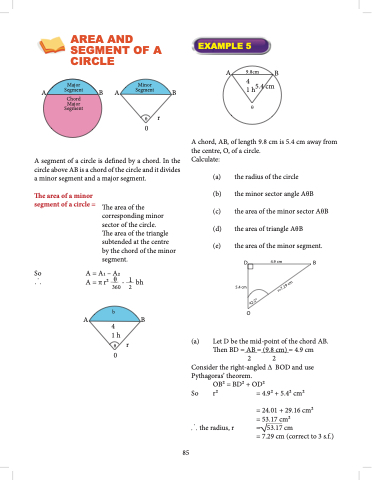
A
9.8cm B 4 5.4 cm
Major A Segment
B A
Minor
Segment B
􏰄r 0
1 h
Chord
Major Segment
􏰄
A segment of a circle is defined by a chord. In the circle above AB is a chord of the circle and it divides a minor segment and a major segment.
A chord, AB, of length 9.8 cm is 5.4 cm away from the centre, O, of a circle.
Calculate:
(a) the radius of the circle
(b) the minor sector angle A􏰄B
(c) the area of the minor sector A􏰄B
(d) the area of triangle A􏰄B
(e) the area of the minor segment.
D 4.9 cm B 5.4 cm
O
The area of a minor segment of a circle =
The area of the corresponding minor sector of the circle.
The area of the triangle subtended at the centre by the chord of the minor segment.
So
A = A1 – A2
A = π r2 􏰄 - bh
360 2
b A4B
1h 􏰄r 0
(a)
Consider the right-angled 􏰅 BOD and use
85
Let D be the mid-point of the chord AB. Then BD = AB = (9.8 cm) = 4.9 cm
Pythagoras’ theorem.
So
r2
the radius, r
= 4.92 + 5.42 cm2
= 53.17 cm2
= 53.17 cm
A=26.5 cm2 h=5.4 cm
A22B
A=39.1 cm
OB2 = BD2 + OD2
O
= 24.01 + 29.16 cm2
b=9.8 cm
= 7.29 cm (correct to 3 s.f.)
42.2o
r=7.29 cm
r=7.29 cm
0=84.40o
..
.
..
.