Page 136 - Sciwie_Katalog

Fächerspezifisches
34
Mathe / Trigonometrie
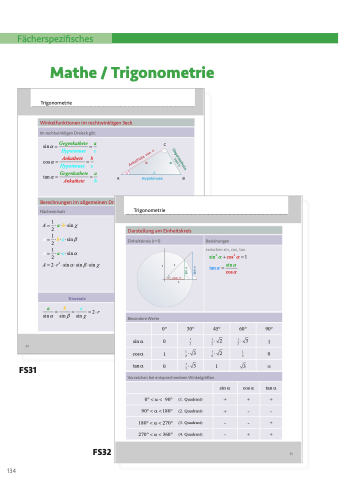
Trigonometrie
Winkelfunktionen im rechtwinkligen 3eck
Im rechtwinkligen Dreieck gilt:
sinα = Gegenkathete = a Hypotenuse c
cosα = Ankathete = b Hypotenuse c
tanα = Gegenkathete = a Ankathete b
􏰔
Sinussatz
a = b = c =2􏰤r sinα sin β sin χ
􏰍
􏰂
􏰃 􏰄􏰅􏰆􏰇􏰈􏰉􏰊􏰋􏰌􏰉
􏰁
􏰓
Berechnungen im allgemeinen Dreieck
Flächeninhalt
A = 1 􏰤 a 􏰤 b 􏰤 sin χ 2
A= 1􏰤b􏰤c􏰤sinβ 2
A = 1 􏰤a􏰤c􏰤sinα 2
A=2􏰤r2 􏰤sinα􏰤sinβ􏰤sinχ
Trigonometrie
􏰔
􏰒
Darstellung am Einheitskreis
􏰂
􏰁
Einheitskreis (r=1)
􏰏 􏰏􏰂
􏰃
􏰏􏰁
􏰖
􏰁􏰝 􏰂􏰓
􏰍􏰃􏰡􏰡 􏰃􏰇􏰌
􏰡
Beziehungen
zwischen sin, cos, tan
sin2 α 􏰥cos2 α =1
tanα = sinα cos α
Cosinussatz
a2 =b2 􏰥c2 􏰦2bc􏰤cosα b2 =a2 􏰥c2 􏰦2ac􏰤cosβ
Besondere Werte
c2 =a2 􏰥b2 􏰦2ab􏰤cosχ 0􏰧
30􏰧 45􏰧 60􏰧 90􏰧
sinα 0 1 1􏰤2 1􏰤3 1 222
cosα 1 1􏰤3 1􏰤2 1 0 222
FS31
tanα 0 13􏰤3 1 3 􏰨
Vorzeichen bei entsprechnednen Winkelgrößen
0􏰧􏰩α􏰩 90􏰧 (1.Quadrant) + + +
90􏰧􏰩α􏰩180􏰧 (2.Quadrant) + - -
180􏰧􏰩α􏰩270􏰧 (3.Quadrant) - - +
270􏰧􏰩α􏰩360􏰧 (4.Quadrant) - + +
sinα cosα tanα
134
FS32
35
􏰑􏰉􏰒􏰉􏰊􏰎􏰁􏰈􏰏􏰉􏰈􏰉 􏰐􏰇􏰊
􏰍􏰊􏰎􏰁􏰈􏰏􏰉􏰈􏰉 􏰐􏰇􏰊
􏰌􏰚􏰊
􏰈􏰁􏰊