Page 247 - Modul Ajar Informatika SMA XII

(SAP-K11-05-U) Ayo Berlatih: Mengunjungi Kebun Binatang
Untuk menyelesaikan permasalahan ini, kita dapat menerapkan prinsip greedy sebagai berikut:
untuk dapat mengunjungi sebanyak-banyaknya atraksi hewan, Dina harus selalu memilih (dari
pilihan yang tersisa) atraksi yang akan selesai paling dulu. Oleh karena itu, akan memudahkan
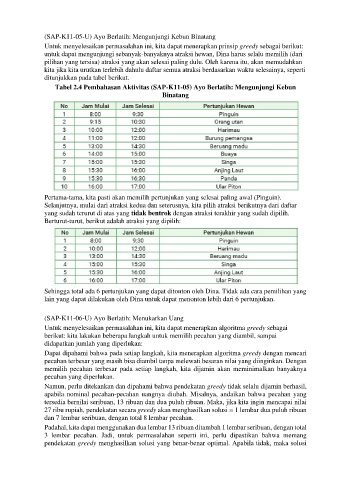
kita jika kita urutkan terlebih dahulu daftar semua atraksi berdasarkan waktu selesainya, seperti
ditunjukkan pada tabel berikut.
Tabel 2.4 Pembahasan Aktivitas (SAP-K11-05) Ayo Berlatih: Mengunjungi Kebun
Binatang

Pertama-tama, kita pasti akan memilih pertunjukan yang selesai paling awal (Pinguin).
Selanjutnya, mulai dari atraksi kedua dan seterusnya, kita pilih atraksi berikutnya dari daftar
yang sudah terurut di atas yang tidak bentrok dengan atraksi terakhir yang sudah dipilih.
Berturut-turut, berikut adalah atraksi yang dipilih:

Sehingga total ada 6 pertunjukan yang dapat ditonton oleh Dina. Tidak ada cara pemilihan yang
lain yang dapat dilakukan oleh Dina untuk dapat menonton lebih dari 6 pertunjukan.

(SAP-K11-06-U) Ayo Berlatih: Menukarkan Uang
Untuk menyelesaikan permasalahan ini, kita dapat menerapkan algoritma greedy sebagai
berikut: kita lakukan beberapa langkah untuk memilih pecahan yang diambil, sampai
didapatkan jumlah yang diperlukan:
Dapat dipahami bahwa pada setiap langkah, kita menerapkan algoritma greedy dengan mencari
pecahan terbesar yang masih bisa diambil tanpa melewati besaran nilai yang diinginkan. Dengan
memilih pecahan terbesar pada setiap langkah, kita dijamin akan meminimalkan banyaknya
pecahan yang diperlukan.
Namun, perlu ditekankan dan dipahami bahwa pendekatan greedy tidak selalu dijamin berhasil,
apabila nominal pecahan-pecahan uangnya diubah. Misalnya, andaikan bahwa pecahan yang
tersedia bernilai seribuan, 13 ribuan dan dua puluh ribuan. Maka, jika kita ingin mencapai nilai
27 ribu rupiah, pendekatan secara greedy akan menghasilkan solusi = 1 lembar dua puluh ribuan
dan 7 lembar seribuan, dengan total 8 lembar pecahan.
Padahal, kita dapat menggunakan dua lembar 13 ribuan ditambah 1 lembar seribuan, dengan total
3 lembar pecahan. Jadi, untuk permasalahan seperti ini, perlu dipastikan bahwa memang
pendekatan greedy menghasilkan solusi yang benar-benar optimal. Apabila tidak, maka solusi