Page 3 - classs 6 a_Neat

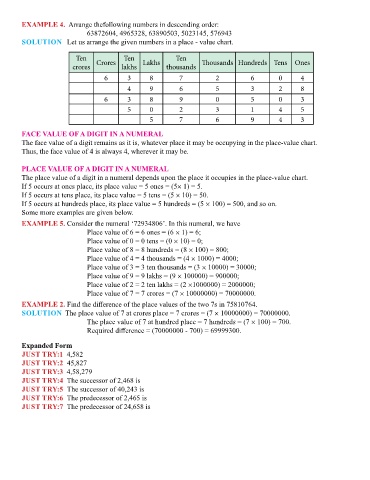
SUCCESSOR OF A WHOLE NUMBER If we add 1 to a whole number, we get the next whole number, EXAMPLE 4. Arrange thefollowing numbers in descending order:
called its successor. Thus, the successor of 0 is 1, the successor of 1 is 2, the successor of 12 is 13, and so on. 63872604, 4965328, 63890503, 5023145, 576943
Every whole number has its successor. SOLUTION Let us arrange the given numbers in a place - value chart.

PREDECESSOR OF A WHOLE NUMBER Ten Crores Ten Lakhs Ten Thousands Hundreds Tens Ones
One less than a given whole number (other than 0), is called its predecessor. Thus, the predecessor of 1 is 0, the crores lakhs thousands
predecessor of2 is 1, the predecessor of 10 is 9, and so on. 6 3 8 7 2 6 0 4
4 9 6 5 3 2 8
The whole number 0 does not have its predecessor.
Every whole number other than 0 has its predecessor. 6 3 8 9 0 5 0 3
5 0 2 3 1 4 5
EXAMPLE 2: Write the successor and predecessor of 5 7 6 9 4 3
(i) 1000 (ii) 1005399 (iii) 999999 FACE VALUE OF A DIGIT IN A NUMERAL
SOLUTION (i) The successor of l000 = (1000 + 1) = 1001. The face value of a digit remains as it is, whatever place it may be occupying in the place-value chart.
The predecessor of l000 = (1000 -1) = 999. Thus, the face value of 4 is always 4, wherever it may be.
(ii) The successor of 1005399 = (1005399 + 1) = 1005400.
The predecessor of l005399 = (1005399 -1) = 1005398. PLACE VALUE OF A DIGIT IN A NUMERAL
(iii)The successor of 999999 = (999999 + 1) = 1000000. The place value of a digit in a numeral depends upon the place it occupies in the place-value chart.
The predecessor of 999999 = (999999 - 1) = 999998 If 5 occurs at ones place, its place value = 5 ones = (5× 1) = 5.
EXAMPLE 3. Arrange the following numbers in ascending order: If 5 occurs at tens place, its place value = 5 tens = (5 × 10) = 50.
3763214,18340217,984671,3790423,18431056 If 5 occurs at hundreds place, its place value = 5 hundreds = (5 × 100) = 500, and so on.
Some more examples are given below.
SOLUTION Let us arrange the given numbers in a place-value chart, as shown below. EXAMPLE 5. Consider the numeral ‘72934806’. In this numeral, we have
Place value of 6 = 6 ones = (6 × 1) = 6;
Crores Ten lakhs Lakhs Ten thousands Thousands Hundreds Tens Ones Place value of 0 = 0 tens = (0 × 10) = 0;
3 7 6 3 2 1 4 Place value of 8 = 8 hundreds = (8 × 100) = 800;
Place value of 4 = 4 thousands = (4 × 1000) = 4000;
1 8 3 4 0 2 1 7
Place value of 3 = 3 ten thousands = (3 × 10000) = 30000;
9 8 4 6 7 1 Place value of 9 = 9 lakhs = (9 × 100000) = 900000;
3 7 9 0 4 2 3 Place value of 2 = 2 ten lakhs = (2 ×1000000) = 2000000;
Place value of 7 = 7 crores = (7 × 10000000) = 70000000.
1 8 4 3 1 0 5 6
EXAMPLE 2. Find the difference of the place values of the two 7s in 75810764.
Out of the given numbers one is a 6 - digit number, two are 7-digit numbers and SOLUTION The place value of 7 at crores place = 7 crores = (7 × 10000000) = 70000000.
two are 8 - digit numbers. The place value of 7 at hundred place = 7 hundreds = (7 × 100) = 700.
6 - digit number is 984671. Required difference = (70000000 - 700) = 69999300.
In 7- digit numbers we have 3763214 < 3790423.
In 8 - digit numbers we have 18340217 < 18431056. Expanded Form
Hence, the given numbers in ascending order are: JUST TRY:1 4,582
984671 < 3763214 < 3790423 < 18340217 < 18431056. JUST TRY:2 45,827
JUST TRY:3 4,58,279
JUST TRY:4 The successor of 2,468 is
JUST TRY:5 The successor of 40,243 is
JUST TRY:6 The predecessor of 2,465 is
JUST TRY:7 The predecessor of 24,658 is