Page 43 - Diktat Fisika SMA Kelas X

v
Q  2 Percepatan sesaat (misal saat di titik P atau Q)
dapat dihitung dengan rumus:
P  1
a  tan  …………………………. 2.21

t 1 t 2 t Dengan  adalah sudut yang dibentuk oleh garis
singgung grafik terhadap waktu t, dihitung dari
Gambar 2.7 Percepatan sesaat pada grafik v-t, sumbu t, berlawanan arah perputaran jarum jam.
a
a  tan  dan  tan  ,

E. Gerak Lurus Beraturan (GLB)

Gerak lurus beraturan (GLB) ialah gerak suatu benda yang lintasannya berupa garis
lurus dan kecepatannya setiap saat selalu tetap. Yang dimaksud, kecepatan tetap pada gerak
lurus beraturan adalah besar kecepatan atau kelajuan dan arah geraknya selalu tetap. Gerak
lurus beraturan juga dapat didefinisikan sebagai gerak suatu benda yang lintasannya lurus dan
dalam waktu yang sama akan menempuh jarak yang sama. Dirumuskan:

Dengan:
 x x  x v = kecepatan / velocity (m/s)
v   2 1 …………… 2.27 x = perpindahan (m/s)
t  t  t 1
2
t = selang waktu (sekon)

Perhatikan grafik hubungan antara kecepatan (v) dan selang waktu (t), di bawah ini!

v (m/s)
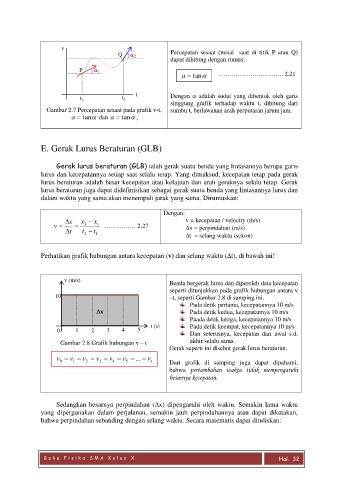
Benda bergerak lurus dan diperoleh data kecepatan
10 seperti ditunjukkan pada grafik hubungan antara v
–t, seperti Gambar 2.8 di samping ini.
Pada detik pertama, kecepatannya 10 m/s
x Pada detik kedua, kecepatannya 10 m/s
Paada detik ketiga, kecepatannya 10 m/s
0 1 2 3 4 5 t (s) Pada detik keempat, kecepatannya 10 m/s
Dan seterusnya, kecepatan dari awal s.d.
Gambar 2.8 Grafik hubungan v – t akhir selalu sama.
Gerak seperti ini disebut gerak lurus beraturan.
v  v  v  v  v  v  ...  v Dari grafik di samping juga dapat dipahami,
2
3
t
5
4
1
0
bahwa pertambahan waktu tidak mempengaruhi
besarnya kecepatan.

Sedangkan besarnya perpindahan (x) dipengaruhi oleh waktu. Semakin lama waktu
yang dipergunakan dalam perjalanan, semakin jauh perpindahannya atau dapat dikatakan,
bahwa perpindahan sebanding dengan selang waktu. Secara matematis dapat dituliskan:

B u k u F i s i k a S M A K e l a s X Hal. 32