Page 240 - Matematica 1° Sec

Capítulo 17
Razones trigonométricas de

ángulos notables III

RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS NOTABLES

¿Se puede calcular la
medida de los lados ¿Qué significa resolver
del triángulo conocien- un triángulo?
do sólo sus ángulos?
60º
30º

Ten presente
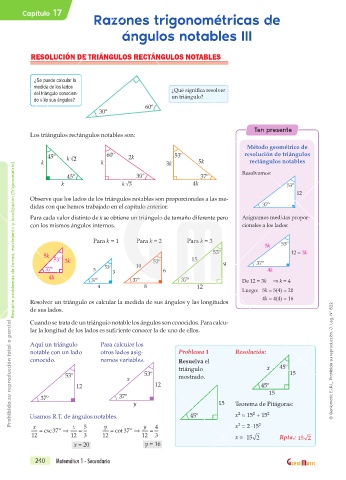
Los triángulos rectángulos notables son:

Método geométrico de
45º k 2 60º 2k 53º resolución de triángulos
k k 3k 5k rectángulos notables
Resuelve problemas de forma, movimiento y localización (Trigonometría)
45º 30º 37º Resolvamos:
k k 3 4k 53º
12
Observe que los lados de los triángulos notables son proporcionales a las me-
didas con que hemos trabajado en el capítulo anterior. 37º
Para cada valor distinto de k se obtiene un triángulo de tamaño diferente pero Asignamos medidas propor-
con los mismos ángulos internos. cionales a los lados:

Para k = 1 Para k = 2 Para k = 3
5k 53º
53º 12 = 3k
5k
53º 3k 53º 15 37º
37º 5 53º 3 10 6 9 4k
4k
37º 37º 37º De 12 = 3k  k = 4
4 8 12
Luego: 5k = 5(4) = 20
4k = 4(4) = 16
Resolver un triángulo es calcular la medida de sus ángulos y las longitudes
de sus lados.

Cuando se trata de un triángulo notable los ángulos son conocidos. Para calcu-
Prohibida su reproducción total o parcia l
lar la longitud de los lados es suficiente conocer la de uno de ellos.

Aquí un triángulo Para calcular los
notable con un lado otros lados asig- Problema 1 Resolución:
conocido. namos variables. Resuelva el  Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
triángulo x 45º
53º 53º mostrado. 15
x
12 12 45º
15
37º 37º
y 15 Teorema de Pitágoras:
2
2
Usamos R.T. de ángulos notables. 45º x = 15 + 15 2
2
x = csc 37 ⇒ x = 5 y = cot 37 ⇒º y = 4 x = 2 ⋅15 2
º
12 12 3 12 12 3 x = 15 2 Rpta.: 15 2
x = 20 y = 16

240 Matemática 1 - Secundaria