Page 94 - RM 1° Sec
P. 94
Capítulo 21
Recorridos eulerianos
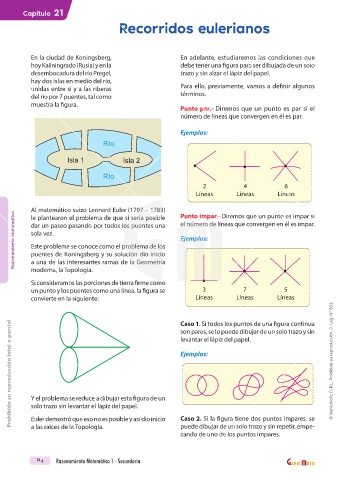
En la ciudad de Koningsberg, En adelante, estudiaremos las condiciones que
hoy Kaliningrado (Rusia) y en la debe tener una figura para ser dibujada de un solo
desembocadura del río Pregel, trazo y sin alzar el lápiz del papel.
hay dos islas en medio del río,
unidas entre sí y a las riberas Para ello, previamente, vamos a definir algunos
del río por 7 puentes, tal como términos.
muestra la figura.
Punto par.- Diremos que un punto es par si el
número de líneas que convergen en él es par.
Ejemplos:
Río
Isla 1 Isla 2
Río
2 4 6
Líneas Líneas Líneas
Al matemático suizo Leonard Euler (1707 – 1783) Punto impar.- Diremos que un punto es impar si
Razonamiento Matemático dar un paseo pasando por todos los puentes una Ejemplos:
le plantearon el problema de que si sería posible
el número de líneas que convergen en él es impar.
sola vez.
Este problema se conoce como el problema de los
puentes de Koningsberg y su solución dio inicio
a una de las interesantes ramas de la Geometría
moderna, la Topología.
Si consideramos las porciones de tierra firme como
un punto y los puentes como una línea, la figura se 3 7 5
convierte en la siguiente: Líneas Líneas Líneas
Caso 1. Si todos los puntos de una figura continua
Prohibida su reproducción total o parcia l
son pares, se lo puede dibujar de un solo trazo y sin
levantar el lápiz del papel.
Ejemplos: Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
Y el problema se reduce a dibujar esta figura de un
solo trazo sin levantar el lápiz del papel.
Euler demostró que eso no es posible y así dio inicio Caso 2. Si la figura tiene dos puntos impares, se
a las raíces de la Topología. puede dibujar de un solo trazo y sin repetir, empe-
zando de uno de los puntos impares.
94 Razonamiento Matemático 1 - Secundaria