Page 117 - Matematica 2° Sec

Relaciones binarias

rePresentación gráfica
El producto cartesiano se puede representar gráficamente. Consideremos los
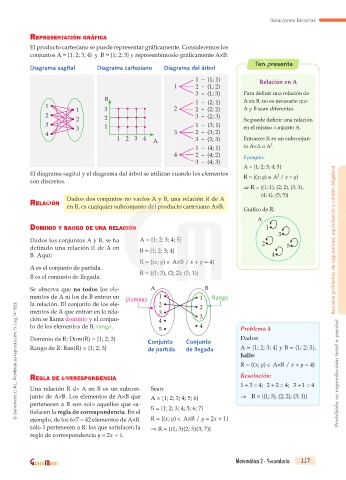
conjuntos A = {1; 2; 3; 4} y B = {1; 2; 3} y representémoslo gráficamente AB:
Ten presente
Diagrama sagital Diagrama cartesiano Diagrama del árbol

1  (1; 1) Relación en A
1 2 – (1; 2)
3 – (1; 3) Para definir una relación de
B 1  (2; 1) A en B, no es necesario que
1 •
• 1 3 2 2 – (2; 2) A y B sean diferentes.
2 • 3 – (2; 3)
• 2 2 Se puede definir una relación
3 • 1 1  (3; 1)
• 3 en el mismo conjunto A.
4 • 3 2 – (3; 2)
1 2 3 4 A 3 – (3; 3) Entonces  es un subconjun-
2
1  (4; 1) to AA o A .
4 2 – (4; 2) Ejemplo:
3 – (4; 3)
A = {1; 2; 3; 4; 5}
El diagrama sagital y el diagrama del árbol se utilizan cuando los elementos R = {(x; y)  A / x = y}
2
son discretos.
 R = {(1; 1), (2; 2), (3; 3),
(4; 4), (5; 5)}
Dados dos conjuntos no vacíos A y B, una relación R de A
relación
en B, es cualquier subconjunto del producto cartesiano AB. Gráfico de R:
A
dominio y rango de una relación 1•
3•
Dados los conjuntos A y B, se ha A = {1; 2; 3; 4; 5} 2• Resuelve problemas de regularidad, equivalencia y cambio (Álgebra)
definido una relación  de A en B = {1; 2; 3; 4} 5•
B. Aquí: 4•
R = {(x; y)  AB / x + y = 4}
A es el conjunto de partida.
B es el conjunto de llegada. R = {(1; 3), (2; 2); (3; 1)}
Se observa que no todos los ele- A B
mentos de A ni los de B entran en Dominio 1 • • 1 Rango
la relación. El conjunto de los ele- 2 • • 2
 Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
mentos de A que entran en la rela- 3 •
ción se llama dominio y el conjun- 4 • • 3
to de los elementos de B, rango. 5 • • 4 Problema 4
Dominio de R: Dom(R) = {1; 2; 3} Conjunto Conjunto Dados:
Rango de R: Ran(R) = {1; 2; 3} de partida de llegada A = {1; 2; 3; 4} y B = {1; 2; 3},
halle:
R = {(x; y)  AB / x + y = 4}
regla de corresPondencia Resolución: Prohibida su reproducción total o parcial
1 + 3 = 4; 2 + 2 = 4; 3 + 1 = 4
Una relación R de A en B es un subcon- Sean:
junto de AB. Los elementos de AB que A = {1; 2; 3; 4; 5; 6}  R = {(1; 3), (2; 2), (3; 1)}
pertenecen a R son solo aquellos que sa-
tisfacen la regla de correspondencia. En el B = {1; 2; 3; 4; 5; 6; 7}
ejemplo, de los 67 = 42 elementos de AB, R = {(x; y)  AB / y = 2x + 1}
sólo 3 pertenecen a R: los que satisfacen la  R = {(1; 3)(2; 5)(3; 7)}
regla de correspondencia y = 2x + 1.

Matemática 2 - Secundaria 117