Page 123 - Matematica 2° Sec
P. 123
Capítulo 22
Funciones lineales
¿Se puede deducir
la regla de corres- x f(x)
pondencia de f(x)?
1 2 ¿Una recta vertical
2 5 o una horizontal
3 8 pueden ser la gráfica
4 11 de una función?
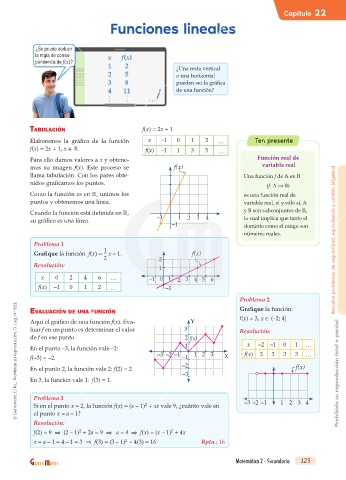
Tabulación f(x) = 2x + 1
Elaboremos la gráfica de la función x –1 0 1 2 Ten presente
f(x) = 2x + 1, x . f(x) –1 1 3 5
Para ello damos valores a x y obtene- Función real de
mos su imagen f(x). Este proceso se f(x) variable real
llama tabulación. Con los pares obte- Una función f de A en B
nidos graficamos los puntos. (f: A B)
Como la función es en , unimos los es una función real de
puntos y obtenemos una línea. variable real, si y sólo si, A
Cuando la función está definida en , y B son subconjuntos de ,
su gráfico es una línea. –1 1 2 3 4 lo cual implica que tanto el
–1 dominio como el rango son
números reales.
Problema 1 Resuelve problemas de regularidad, equivalencia y cambio (Álgebra)
1
Grafique la función f(x) = x – 1. f(x)
2 2
Resolución:
1
x 0 2 4 6 –1 0 1 2 3 4 5 6
f(x) –1 0 1 2 –1
Problema 2
Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
Evaluación dE una función Grafique la función:
Aquí el gráfico de una función f(x). Eva- Y f(x) = 3, x –2; 4
luar f en un punto es determinar el valor 3 Resolución:
de f en ese punto. 2 f(x)
En el punto –3, la función vale –2: 1 x –2 –1 0 1
–3 –2 –1 1 2 3 f(x) 3 3 3 3
f(–3) = –2. –1 X
–2
En el punto 2, la función vale 2: f(2) = 2 f(x)
–3 Prohibida su reproducción total o parcial
En 3, la función vale 1: f(3) = 1.
Problema 3
2
Si en el punto x = 2, la función f(x) = (x – 1) + ax vale 9, ¿cuánto vale en –3 –2 –1 1 2 3 4
el punto x = a – 1?
Resolución:
2
2
f(2) = 9 (2 – 1) + 2a = 9 a = 4 f(x) = (x – 1) + 4x
2
x = a – 1 = 4 – 1 = 3 f(3) = (3 – 1) + 4(3) = 16 Rpta.: 16
Matemática 2 - Secundaria 123