Page 169 - Do it! 자료구조와 함께 배우는 알고리즘(C 언어, 3쇄)

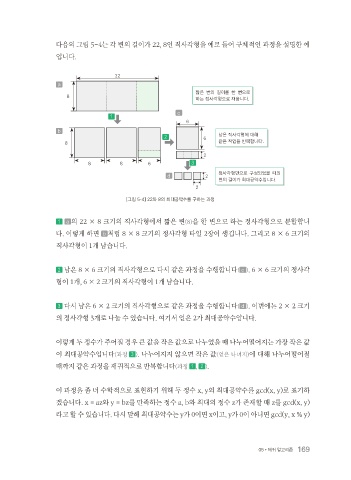
다음의 그림 5-4는 각 변의 길이가 22, 8인 직사각형을 예로 들어 구체적인 과정을 설명한 예

입니다.

22
a
짧은 변의 길이를 한 변으로
8
하는 정사각형으로 채웁니다.
c
1
6
b
2 6 남은 직사각형에 대해
8 같은 작업을 반복합니다.
2
8 8 6 3
정사각형만으로 구성되었을 때의
d 2
변의 길이가 최대공약수입니다.
2
[그림 5-4] 22와 8의 최대공약수를 구하는 과정

1 a 의 22 × 8 크기의 직사각형에서 짧은 변(8)을 한 변으로 하는 정사각형으로 분할합니
다. 이렇게 하면 b 처럼 8 × 8 크기의 정사각형 타일 2장이 생깁니다. 그리고 8 × 6 크기의

직사각형이 1개 남습니다.

2 남은 8 × 6 크기의 직사각형으로 다시 같은 과정을 수행합니다( c ). 6 × 6 크기의 정사각
형이 1개, 6 × 2 크기의 직사각형이 1개 남습니다.

3 다시 남은 6 × 2 크기의 직사각형으로 같은 과정을 수행합니다( d ). 이번에는 2 × 2 크기
의 정사각형 3개로 나눌 수 있습니다. 여기서 얻은 2가 최대공약수입니다.

이렇게 두 정수가 주어질 경우 큰 값을 작은 값으로 나누었을 때 나누어떨어지는 가장 작은 값
이 최대공약수입니다(과정 3 ). 나누어지지 않으면 작은 값(얻은 나머지)에 대해 나누어떨어질
때까지 같은 과정을 재귀적으로 반복합니다(과정 1 , 2 ).

이 과정을 좀 더 수학적으로 표현하기 위해 두 정수 x, y의 최대공약수를 gcd(x, y)로 표기하
겠습니다. x = az와 y = bz를 만족하는 정수 a, b와 최대의 정수 z가 존재할 때 z를 gcd(x, y)

라고 할 수 있습니다. 다시 말해 최대공약수는 y가 0이면 x이고, y가 0이 아니면 gcd(y, x % y)

05•재귀 알고리즘 169