Page 20 - Do it! 자료구조와 함께 배우는 알고리즘(C 언어, 3쇄)

보충수업 1-4 세 값의 대소 관계와 중앙값

세 값의 대소 관계는 13종류
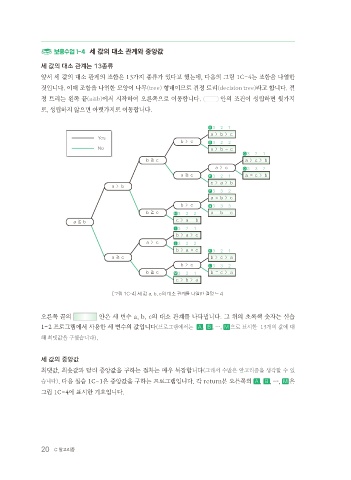
앞서 세 값의 대소 관계의 조합은 13가지 종류가 있다고 했는데, 다음의 그림 1C-4는 조합을 나열한
것입니다. 이때 조합을 나열한 모양이 나무(tree) 형태이므로 결정 트리(decision tree)라고 합니다. 결
정 트리는 왼쪽 끝(a≧b)에서 시작하여 오른쪽으로 이동합니다. 안의 조건이 성립하면 윗가지
로, 성립하지 않으면 아랫가지로 이동합니다.

A 3 2 1
a ＞ b ＞ c
Yes
b ＞ c B 3 2 2
No a ＞ b ＝ c
C 3 2 1
b ≧ c a ＞ c ＞ b
a ＞ c D 3 3 2
a ≧ c E 3 2 1 a ＝ c ＞ b
c ＞ a ＞ b
a ＞ b
F 3 3 2
a ＝ b ＞ c
b ＞ c G 3 3 3
b ≧ c H 3 2 2 a ＝ b ＝ c
a ≧ b c ＞ a ＝ b
I 3 2 1
b ＞ a ＞ c
a ＞ c J 3 2 2
b ＞ a ＝ c K 3 2 1
a ≧ c b ＞ c ＞ a
b ＞ c L 3 3 2
b ≧ c M 3 2 1 b ＝ c ＞ a
c ＞ b ＞ a

[그림 1C-4] 세 값 a, b, c의 대소 관계를 나열한 결정 트리

오른쪽 끝의 안은 세 변수 a, b, c의 대소 관계를 나타냅니다. 그 위의 초록색 숫자는 실습
1-2 프로그램에서 사용한 세 변수의 값입니다(프로그램에서는 A , B , …, M 으로 표시한 13개의 값에 대
해 최댓값을 구했습니다).

세 값의 중앙값
최댓값, 최솟값과 달리 중앙값을 구하는 절차는 매우 복잡합니다(그래서 수많은 알고리즘을 생각할 수 있
습니다). 다음 실습 1C-1은 중앙값을 구하는 프로그램입니다. 각 return문 오른쪽의 A , B , …, M 은
그림 1C-4에 표시한 기호입니다.

20 C 알고리즘