Page 81 - Do it! 자료구조와 함께 배우는 알고리즘(C 언어, 3쇄)

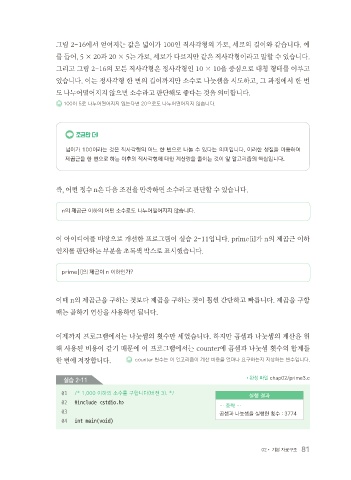
그림 2-16에서 얻어지는 값은 넓이가 100인 직사각형의 가로, 세로의 길이와 같습니다. 예

를 들어, 5 × 20과 20 × 5는 가로, 세로가 다르지만 같은 직사각형이라고 말할 수 있습니다.
그리고 그림 2-16의 모든 직사각형은 정사각형인 10 × 10을 중심으로 대칭 형태를 이루고
있습니다. 이는 정사각형 한 변의 길이까지만 소수로 나눗셈을 시도하고, 그 과정에서 한 번
도 나누어떨어지지 않으면 소수라고 판단해도 좋다는 것을 의미합니다.

100이 5로 나누어떨어지지 않는다면 20으로도 나누어떨어지지 않습니다.

조금만 더!
넓이가 100이라는 것은 직사각형의 어느 한 변으로 나눌 수 있다는 의미입니다. 이러한 성질을 이용하여
제곱근을 한 변으로 하는 이후의 직사각형에 대한 계산량을 줄이는 것이 앞 알고리즘의 핵심입니다.

즉, 어떤 정수 n은 다음 조건을 만족하면 소수라고 판단할 수 있습니다.

n의 제곱근 이하의 어떤 소수로도 나누어떨어지지 않습니다.

이 아이디어를 바탕으로 개선한 프로그램이 실습 2-11입니다. prime[i]가 n의 제곱근 이하
인지를 판단하는 부분을 초록색 박스로 표시했습니다.

prime[i]의 제곱이 n 이하인가?

이때 n의 제곱근을 구하는 것보다 제곱을 구하는 것이 훨씬 간단하고 빠릅니다. 제곱을 구할
때는 곱하기 연산을 사용하면 됩니다.

이제까지 프로그램에서는 나눗셈의 횟수만 세었습니다. 하지만 곱셈과 나눗셈의 계산을 위
해 사용된 비용이 같기 때문에 이 프로그램에서는 counter에 곱셈과 나눗셈 횟수의 합계를
한 번에 저장합니다. counter 변수는 이 알고리즘이 계산 비용을 얼마나 요구하는지 저장하는 변수입니다.

실습 2-11 •완성 파일 chap02/prime3.c

01 /* 1,000 이하의 소수를 구합니다(버전 3). */
실행 결과
02 #include <stdio.h>
… 중략 …
03 곱셈과 나눗셈을 실행한 횟수 : 3774
04 int main(void)

02• 기본 자료구조 81