Page 160 - NUMINO Challenge_M1
P. 160
Problem solving
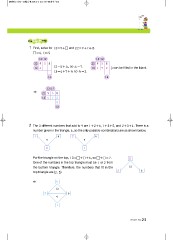
1 First, solve for 13=9+ and 22=9+ +8.
=4, =5
13 12 12=5+ , so =7. 13 12 3 can be filled in the blank.
22 9 5 8 13=4+7+ so =2. 22 9 5 8
13 4 13 4 7 2
13 13
13 12
22 9 5 8
13 4 7 2
3
13
2 The 3 different numbers that add to 9 are 1+2+6, 1+3+5, and 2+3+4. There is a
number given in the triangle, 6, so the only possible combinations are as shown below.
16 26
9 9
21
For the triangle on the top, 13= + +6, so + =7. 5
One of the numbers in the top triangle must be 1 or 2 from
the bottom triangle. Therefore, the numbers that fit in the 13
top triangle are (2, 5). 26
5
13
26
9
1
23Answer Key
1 First, solve for 13=9+ and 22=9+ +8.
=4, =5
13 12 12=5+ , so =7. 13 12 3 can be filled in the blank.
22 9 5 8 13=4+7+ so =2. 22 9 5 8
13 4 13 4 7 2
13 13
13 12
22 9 5 8
13 4 7 2
3
13
2 The 3 different numbers that add to 9 are 1+2+6, 1+3+5, and 2+3+4. There is a
number given in the triangle, 6, so the only possible combinations are as shown below.
16 26
9 9
21
For the triangle on the top, 13= + +6, so + =7. 5
One of the numbers in the top triangle must be 1 or 2 from
the bottom triangle. Therefore, the numbers that fit in the 13
top triangle are (2, 5). 26
5
13
26
9
1
23Answer Key