Page 6 - PROJEK BUKU DIGITAL_NATASYA ISABEL BR. SIAHAAN_4191111055_PSPM A 2019
P. 6
Rotasi terhadap titik
pusat ( , )
Rotasi terhadap titik
pusat ( , )
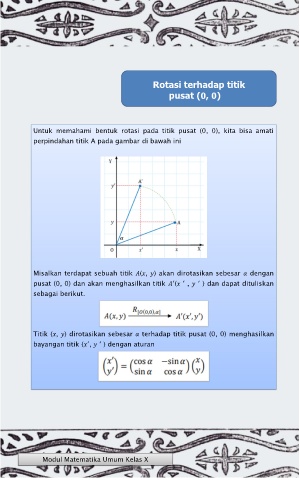
Untuk memahami bentuk rotasi pada titik pusat (0, 0), kita bisa amati
Rotasi terhadap titik
perpindahan titik A pada gambar di bawah ini
pusat ( , )
Misalkan terdapat sebuah titik ( , ) akan dirotasikan sebesar dengan
pusat (0, 0) dan akan menghasilkan titik ′( ′ , ′ ) dan dapat dituliskan
sebagai berikut.
Titik ( , ) dirotasikan sebesar terhadap titik pusat (0, 0) menghasilkan
bayangan titik ( ′, ′ ) dengan aturan
Modul Matematika Umum Kelas X 6