Page 23 - Ebook Interaktif Bilangan Berpangkat

e
a
C Applying et
h
h
e
t
s
E x p o n e n t R u l e
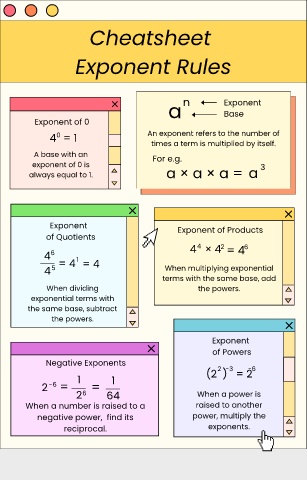
Exponent Ruless
Exponent
a a n n E x a p s o n e n t
Base
e
B
f

0
n

n
p

t
o
e
o
E
Exponent of 0
x

e
o
e
x
f
u
A
m
n
p
e
n
t
s
e
t

o
r
e

n
o

b

n
h
r
t
e
r
=
1

4 = 1 An exponent refers to the number of f
4
0 0
m
t
u
p
l

i
i
times a term is multiplied by itself. .
l
e
t
e
s
i

t
i
m
t
l

r
e
a

e
b
d
i
m
f
s

s
y
n
a
s
e
b
A base with an F o r e . g .
A

h

a
t
w
i
For e.g.
n
e
exponent of 0 is s 3 3
0

f
t

n
e
o

p
x
i
o
a × a × a =
always equal to 1.
a l w a y s e q u a l t o 1 . a × a × a = a a
Exponent
E x p o n e n t E x p o n e n t o f P r o d u c t s
Exponent of Products
of Quotients
o f Q u o t i e n t s
4 4
4 × 4 6 6
4 × 4 = 4 = 4
2 2
4 4 6 6 1 1
= 4 = 4 = 4
y
l
4 4 5 5 = 4 When multiplying exponential l
n
l

h
e
n
n
i
u
a
i
t

g
m
p
W
t
i
x
n
o
e
e
p
t
s
d
a

b
a
h
d
,
e
e
h

s
a
e

m
m
s

r
terms with the same base, add
t
e
i
t
w

s
e
h
r
d
w
o
i
n
n
p

g
When dividing t the powers. .
i
d
h
i
W
v
e
e
exponential terms with
e x p o n e n t i a l t e r m s w i t h
u
b

a
,
e
s
s

s
t
e
r
a
m
a
c
e
b

h
t the same base, subtract t
t the powers. .
o
h
e
e
p
s
w

r
o
n
E
e
n
x
Exponent
t
p
r
w
e
s
o
o

f
P
of Powers
e
N
n
t
E
o
n
g
e
x
p
a

v
e
s
i
Negative Exponents ( 2 2 -3 = 2 6
t
-

2
-
-6
3
(2 ) = 2
)

2 = = 1 1 = = 1 1
-6
6
-
2
2 2 6 6 6 4 When a power is
64
W
h

i
s
r
w
p
n

o
a

e
e
a
r
t

i
a
o

s
o
t
h
e
e
n
d
When a number is raised to a raised to another r
When a number is raised to a p o w e r , m u l t i p l y t h e
power, multiply the
negative power, find its
negative power, find its e x p o n e n t s .
exponents.
reciprocal.
reciprocal.