Page 7 - gg

ل

ا
م ج
a  / 0 P ( ) x  ax  bx ة تيبلا ة خ رد لا ن ذود تار بتك 
2
ا : c
ف عم ل ا

2
a  / 0 ax  bx c  0 ي R تألذا 1 .
2
2
S    0 نذإ x  0 ئفاك ي ax  0 يأ c  0 و b  0 
ax  bx c  0 يأ c  0 و b  0  c  0 و b  0  يأ c  0 و b  0 

2
b 
 2 4ac زيمملا بسحن ax  2 bx  0 يأ 2   c ax  2 c 
ئفاكي ( x ax b  ) 0 x a وأ 0

(  > 0 ( بجوم زيمملا مودعم زيمملا بلاس زيمملا  x  0 c  0 c  0

(  = 0 ( (   0 (  ax b  0 a a

  b       b     b  S    0   b    c   c   S  
S   ;  S    2a   S    a ;0   S   ; 
 2a 2a     a a   

م ع
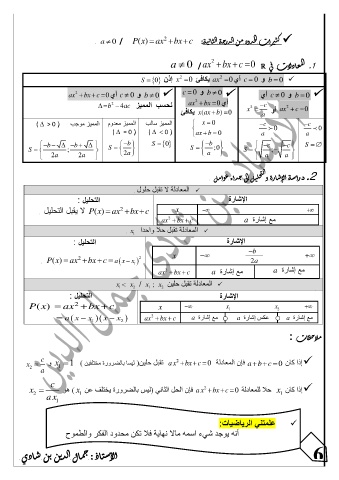
ل او ءاد خ ل بل ح تلا و ةرا أل ا ش ةسار 2 . د
يا ل
لولح لبقت لا ةلداعملا 
: ليلحتلا ةراش ا لإ
ليلحتلا لبقي لا P ( ) x  ax  bx c x    

2
ax  2 bx c a ةراشإ عم

x 1 ادحاو لاح لبقت ةلداعملا 
: ليلحتلا ةراش ا لإ
b

P ( ) x  ax  bx c   a x x 1  2 x   2a  

2

ax  2 bx c a ةراشإ عم a ةراشإ عم

x

x  x 2 / ; x 2 نيلح لبقت ةلداعملا 
1
1
: ليلحتلا ةراشلإا
( ) 
2
P x ax  bx  c x  
x
x
2
1

a  x  x 1  x  x 2  ax  2 bx c a ةراشإ عم a ةراشإ سكع a ةراشإ عم
م
طح
: تا ال
x  c و x  ) 1 نيفلتخم ةرورضلاب اسيل ) نيلح لبقت ax  bx c  0 ةلداعملا نإف a b c  0 ناك اذإ 


2

2 1
a
c
x  وه ) x نع فلتخي ةرورضلاب سيل( يناثلا لحلا نإف ax  bx c  0 ةلداعملل لاح x ناك اذإ 

2
2
a x 1 1 1

: تايضايرلا ينتملع 
حومطلاو ركفلا دودحم نكت لاف ةياهن لاام همسا ءيش دجو ي هنأ

بس

ش ي ي لا لا
ن
يذا ن د مج : ذا ألا 6