Page 122 - Algebra
P. 122

6.4. Graphing Quadratic Equations
The graph of the quadratic equation f(x) = ax2 + bx + c = 0, where a =ΜΈ 0 is a parabola.
β€’ If a < 0, the graph opens upward.
β€’ If a > 0, the graph opens downward.
βˆ’π‘ βˆ’π‘
β€’ The maximum or the minimum point of the parabola is called the vertex. βˆ’π‘
β€’ The line of symmetry is x = 2π‘Ž
β€’ The coordinates of the vertex are (2π‘Ž, f(2π‘Ž))
β€’ When a > 0, a quadratic equation has a minimum value that occurs at x =
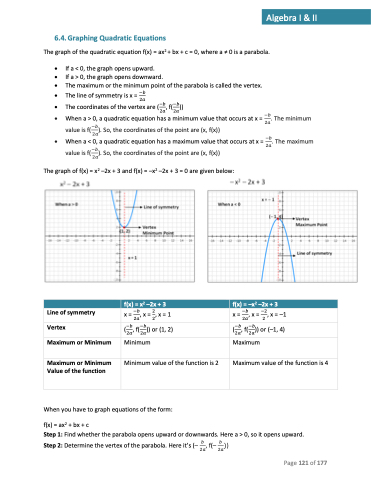
 β€’ When a < 0, a quadratic equation has a maximum value that occurs at x = The graph of f(x) = x2 –2x + 3 and f(x) = –x2 –2x + 3 = 0 are given below:
βˆ’π‘
2π‘Ž. The minimum
 βˆ’π‘
value is f( 2π‘Ž). So, the coordinates of the point are (x, f(x))
 βˆ’π‘
2π‘Ž. The maximum
 βˆ’π‘
value is f( 2π‘Ž). So, the coordinates of the point are (x, f(x))
      f(x)=x2 –2x+3
   f(x)=–x2 –2x+3
 Line of symmetry Vertex
Maximum or Minimum
βˆ’π‘ 2
x = 2π‘Ž, x = 2, x = 1
βˆ’π‘ βˆ’π‘
(2π‘Ž, f(2π‘Ž)) or (1, 2)
Minimum
βˆ’π‘ βˆ’2
x = 2π‘Ž, x = 2 , x = –1
βˆ’π‘ βˆ’π‘
(2π‘Ž, f(2π‘Ž)) or (–1, 4)
Maximum
         Maximum or Minimum Value of the function
   Minimum value of the function is 2
   Maximum value of the function is 4
 When you have to graph equations of the form: f(x)=ax2 +bx+c
Step 1: Find whether the parabola opens upward or downwards. Here a > 0, so it opens upward.
Step 2: Determine the vertex of the parabola. Here it’s (– , f(– )) 2π‘Ž 2π‘Ž
𝑏𝑏
Page 121 of 177
 Algebra I & II
   120   121   122   123   124