Page 124 - Algebra

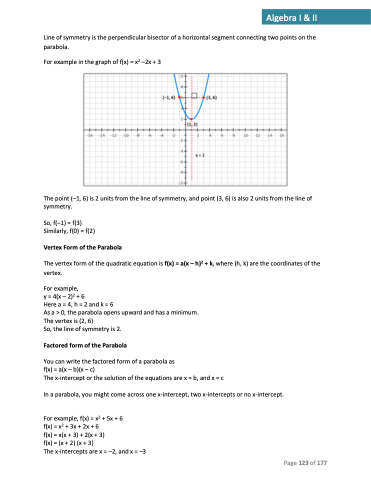
Line of symmetry is the perpendicular bisector of a horizontal segment connecting two points on the parabola.
For example in the graph of f(x) = x2 –2x + 3
The point (–1, 6) is 2 units from the line of symmetry, and point (3, 6) is also 2 units from the line of symmetry.
So, f(–1) = f(3) Similarly, f(0) = f(2)
Vertex Form of the Parabola
The vertex form of the quadratic equation is f(x) = a(x – h)2 + k, where (h, k) are the coordinates of the
vertex.
For example,
y = 4(x – 2)2 + 6
Here a = 4, h = 2 and k = 6
As a > 0, the parabola opens upward and has a minimum. The vertex is (2, 6)
So, the line of symmetry is 2.
Factored form of the Parabola
You can write the factored form of a parabola as
f(x) = a(x – b)(x – c)
The x-intercept or the solution of the equations are x = b, and x = c
In a parabola, you might come across one x-intercept, two x-intercepts or no x-intercept.
For example, f(x) = x2 + 5x + 6 f(x) = x2 + 3x + 2x + 6
f(x) = x(x + 3) + 2(x + 3)
f(x) = (x + 2) (x + 3)
The x-intercepts are x = –2, and x = –3
Page 123 of 177
Algebra I & II