Page 11 - Curvas de gato

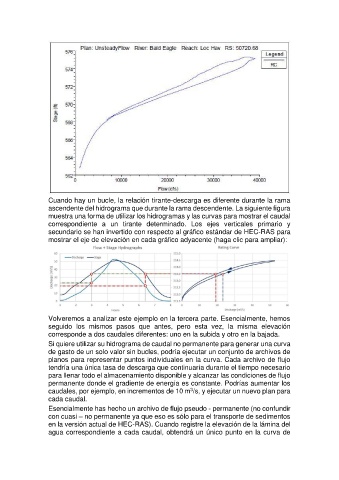
Cuando hay un bucle, la relación tirante-descarga es diferente durante la rama
ascendente del hidrograma que durante la rama descendente. La siguiente figura
muestra una forma de utilizar los hidrogramas y las curvas para mostrar el caudal
correspondiente a un tirante determinado. Los ejes verticales primario y
secundario se han invertido con respecto al gráfico estándar de HEC-RAS para
mostrar el eje de elevación en cada gráfico adyacente (haga clic para ampliar):

Volveremos a analizar este ejemplo en la tercera parte. Esencialmente, hemos
seguido los mismos pasos que antes, pero esta vez, la misma elevación
corresponde a dos caudales diferentes: uno en la subida y otro en la bajada.
Si quiere utilizar su hidrograma de caudal no permanente para generar una curva
de gasto de un solo valor sin bucles, podría ejecutar un conjunto de archivos de
planos para representar puntos individuales en la curva. Cada archivo de flujo
tendría una única tasa de descarga que continuaría durante el tiempo necesario
para llenar todo el almacenamiento disponible y alcanzar las condiciones de flujo
permanente donde el gradiente de energía es constante. Podrías aumentar los
caudales, por ejemplo, en incrementos de 10 m /s, y ejecutar un nuevo plan para
3
cada caudal.
Esencialmente has hecho un archivo de flujo pseudo - permanente (no confundir
con cuasi – no permanente ya que eso es sólo para el transporte de sedimentos
en la versión actual de HEC-RAS). Cuando registre la elevación de la lámina del
agua correspondiente a cada caudal, obtendrá un único punto en la curva de