Page 8 - Dạy - học trực tuyến

90% kiến thức lớp 12 8 Gv. Phạm Văn Rô
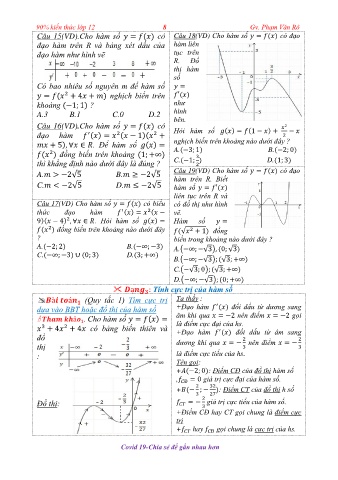
Câu 15(VD).Cho hàm số ( ) có Câu 18(VD) Cho hàm số ( ) có đạo
đạo hàm trên R và bảng xét dấu của hàm liên
đạo hàm như hình vẽ tục trên
R. Đồ
thị hàm
số
Có bao nhiêu số nguyên m để hàm số
( ) nghịch biến trên ( )

khoảng ( ) ? như
A.3 B.1 C.0 D.2 hình
bên.
Câu 16(VD).Cho hàm số ( ) có

đạo hàm ( ) ( )( Hỏi hàm số ( ) ( )
) . Để hàm số ( ) nghịch biến trên khoảng nào dưới đây ?
B.( )
A.( )

( ) đồng biến trên khoảng ( )
thì khẳng định nào dưới đây là đúng ? C.( ) D.( )

A. √ B. √ Câu 19(VD) Cho hàm số ( ) có đạo
hàm trên R. Biết
C. √ D. √ hàm số ( )
liên tục trên R và
Câu 17(VD) Cho hàm số ( ) có biểu có đồ thị như hình
thức đạo hàm ( ) ( vẽ.

)( ) . Hỏi hàm số ( ) Hàm số

( ) đồng biến trên khoảng nào dưới đây (√ ) đồng

? biến trong khoảng nào dưới đây ?
A.( ) B.( ) A.( √ ) ( √ )
C.( ) ( ) D.( ) B.( √ ) (√ )

C.( √ ) (√ )
D.( √ ) ( )
 ạ : Tính cực trị của hàm số

 { | (Quy tắc 1) Tìm cực trị Ta thấy :

dựa vào BBT hoặc đồ thị của hàm số +Đạo hàm ( ) đổi dấu từ dương sang
. Cho hàm số ( ) âm khi qua nên điểm gọi
là điểm cực đại của hs.

có bảng biến thiên và +Đạo hàm ( ) đổi dấu từ âm sang

đồ
thị dương khi qua nên điểm

: là điểm cực tiểu của hs.
Tên gọi:
+ ( ): Điểm CĐ của đồ thị hàm số
, giá trị cực đại của hàm số.

+ ( ): Điểm CT của đồ thị h số

Đồ thị: giá trị cực tiểu của hàm số.

+Điểm CĐ hay CT gọi chung là điểm cực
trị
+ hay gọi chung là cực trị của hs.
Covid 19-Chia sẻ để gần nhau hơn hơn