Page 11 - KI - aritmetica 2 sec

Aritmética 2° Secundaria

Adición y sustracción

 Fracciones homogéneas

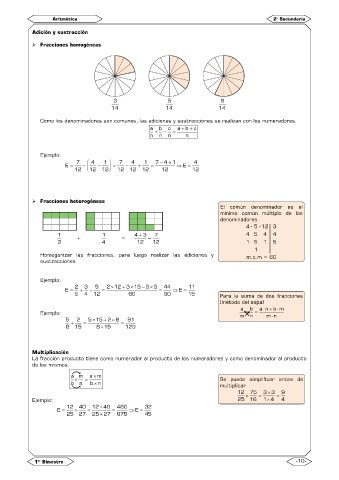
3 5 8

14 14 14

Como los denominadores son comunes, las adiciones y sustracciones se realizan con los numeradores.
a  b  c  a  b  c
n n n n

Ejemplo:


7  4 1  7 4 1 7 4 1 4
E           E 
12  12 12 12 12 12 12 12

 Fracciones heterogéneas
El común denominador es el
mínimo común múltiplo de los
denominadores.
- -
4 5 12 3

1 1 4  3 7 4 5 4 4
+ = 
3 4 12 12 1 5 1 5
1
Homogenizar las fracciones, para luego realizar las adiciones y m.c.m = 60
sustracciones

Ejemplo:




2 3 5 2 12 3 15 5 5 44 11

E       E 
5 4 12 60 60 15 Para la suma de dos fracciones
(método del aspa)
a b a n b m



Ejemplo: m  n  m n




5 2 5 15 2 8 91
  
8 15 8 15 120


Multiplicación
La fracción producto tiene como numerador al producto de los numeradores y como denominador al producto
de los mismos.
a m  a m Se puede simplificar antes de



b n b n
multiplicar

12  75  3 3  9

Ejemplo: 25 16 1 4 4

12 40 12 40 480 32
E      E 

25 27 25 27 675 45

er
1 Bimestre -10-