Page 71 - demo

MATLAB

ونگوس ا ن سا روتوم ا یرادرب هر ب لع یر م م ع او رد نمشوه عاو ش لص م لع هب ا یرادرب هر ب ی نو رش هناری شیپ تاریمعت و یرا ن رد یلمع رو ب
اس یهد ینا مم ا ن سا روتوم رد هک سا یا ) ینا مم یاج هب ( " ر لمع ا یرادرب هر ب اب یس و ه ش ی ارط نمشوه یس ی اس هدایپ درجورب یجا ن تا نا راک رد ؛هع ا م دروم هناری شیپ تاریمعت و یرا ن یارب یعونصم شوه ی ا م نیآرف ی نسرا عا و یبای را ج

تروص هب زادرپ ایم یاه ی باو و باور هب نمشوه عاو عیم ت س و ا ل سا ون ا نا م و سا ید ا ر ن 18 تار ن اب هناگا ج تاعلاطا یروآدرگ را با ی رد قیقحت یا نمشوه یس یاه یجور ؛قیقحت نمشوه یس ی ارط ا عب اوج و اه
قی دان ترو هب یدورو یس یجور یاه ننو ماک یریگ ) ه ی ن و ا ن سا یارب نمشوه عاو یروآدرگ ج ( STEP ییا ن اف رداه یجور لیلحت اگر و اصص م ی هلیسوب و ش هاو
فا ی یا اع ادفا ی باش STEP را فا رن رد ؛ And "
ی دان نمشوه را فا رن رد ا ل سا ون ا نا . یارب ین با و ینیب اب و یبای را دروم ؛ ترم یا نام اس ن ش ه یاقم روک م اگر
STEP هناری شیپ تاریمعت و یرا ن STEP اری : ددر یم یرادرب هر ب Min MATLAB MATLAB 5 ؛ه ش ه ارا م فرگ هاو رار لا ا
اشوپ و یجا ن عیان رد
-
ا
2 3 درجورب یجا ن تا نا راک ان و هاتوک ار یجور ی اف هعوم م Prod ر لمع " نمشوه عاو عیم ت س
4 . یامنیم . ییامنیم ا نا ار " Max و یرا ن " یس یجور ری م نمشوه لیلحت ج لات ا ددرگیم هدهاشم هک رو نامه متسیس دعاو دنمشوه متسیس ساتید و ناگر لات ا سن ییاهن توا ت
یاه ی ور
ساپ یگنایم
درجورب یجا ن
"
تا نا
راک رد هناری شیپ تاریمعت
دنمشوه

نمشوه یس یاه یجور لیلحت هب او یم ا ل ا یا ن گ یاب یا ن رد
نمشوه یس رد دوجوم اس ی افری ره رت قی د وم م تروصنیارد PM-DM-SD-ANFIS م ی ه ارا ا ند هب قیقحت یا متسیس یاه ی ور یب ییاهن
یدربراک و یرتفورعم
.
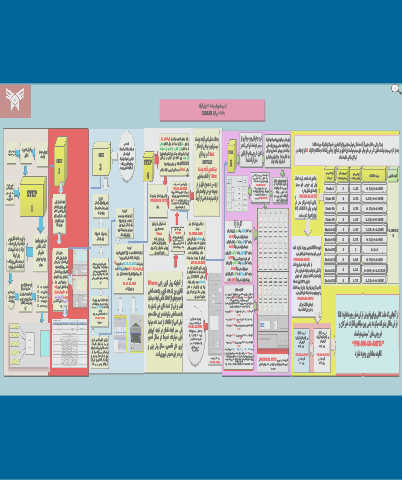
رد ی دان زادرپ یرت PM.DM-SD-ANFIS ادرپ ؛ یناب و ) قی د ( ید ع ترو هب رد هناری شیپ تاریمعت و یرا ن : ینعی یقحت یا دنمشوه Rule3 1 1.22 0.22 ÷ 4=0.055
- یعون م وه متسیس STEP . یامنیم یع د ع ی هب لی ت ار ی اف یجور ر ن رد عاو یجور هعوم م یاهری م ش یمآ را فر لیلحت هب ؛لی ل ش و و ج - اشوپ و یجا ن عن

و ام یجور و یدورو
نمشوه یس
هاگیاپ نمشوه یس ا ن سا روتوم ی ارط رن اس را فا ی افری م ردMATLAB ا اه . آ ا یش ب هن نوشیم ه فرگ : د ادرپ PM-DM-SD-ANFIS هب درجورب یجا ن تا نا راک و PM-DM-SD-ANFIS
یم
؛ وا اگ

-
سا یزاف یناو ی یک یاهری م یرعت شناد ل م ی وت ها یاپ ی ارط PM.DM-SD-ANFIS شور Wtavar ری یا اری ددر یم یرادرب ی اف هر ب . دوش رط یارجا لحم اونع راد ینعم ناگر تار ن یگنایم Rule45 3 2.72 0.28 ÷ 4=0.0675
1 یاه ی ا یرادرب هر ب اب م یعونصم شوه رب ین م ؛ مود ماگ ونگوس یامنیم مک تا ساحم یارب ( 65 .06475 اب ربارب و هدو ن Rule79 3 2.78 0.22 ÷ 4=0.055
ر مک ام ین و ه م یگ ی یپ شهاک هب اس
و دا عا یص ت و یناب

عباوت و ی اف یاه هعوم م نمشوه یایوپ متسیس ی رد دعاو یا یکرت . سا دصرد 7 زا رتمک مرازه )
ون ا نا و یو ع هاگیاپ دعاو ریاس . سا دحاو Rule86 2 1.67 0.33 ÷ 4=0.0825
ا نآ هب ش ج وه رب ینت م ناد ل مدی وت رن اس را فا ی افری م یس ا ن سا روتوم ی ارط رد رگا ( If ) ؛
هب زین دنمشوه متسیس یا یعون م شور ا MATLAB شور هل رم یا رد نمشوه عبات ی اب ارک ن رد " و ( انکراک " لماع یع و Rule103 2 1.67 0.33 ÷ 4=0.0825 0.0647
ها یاپ اس نیآرف هل رم دندش دی وت یترت یا Wtavar wtavar PM-DM-SD-ANFIS 5
یسررب لا ند هب هلحرم یا رد شناد ل م ی وت ددر یم یرادرب هر ب لی ت ج ییاد ی اف یارب ییاد ی اف یارب wtavarr ور 0.9129 اقی د ینعی شاب ) و یو ع Rule140 3 2.78 0.22 ÷ 4=0.055
ه ایوپ یزاس لدم هب ی اف یاه هعوم م و دا عا عبات ی اب ارک یرو نف ن رد " و ( " لماع یع و

،مقایسه وی گی های مت اوت شهاک هب اس ی اف ری یا اری یع او یسررب ج یع را قم ی اف یاه هعوم م و دا عا لی ت ج
ییاسانش و شک ؛ وس اگ یارب ر مک ام ین و ه م یگ ی یپ . سا ه ش ا نا یس در لمع یع او یسررب ج و یع را قم هب 0.9239 اقی د ینعی شاب ) و یو ع ه یاقم هب او یم ؛دوجوم ی ی وت تاعلاطا هب هجوت اب
ن ننو ماک هدش دزمان لدم Rule157 3 3 ÷ 0 4=0
یاهریی تم لکش و لود تاریمعت و یرا ن " و ام نمشوه عاو دا عت یا ن رد یامنیم مک تا ساحم . سا ه ش ا نا یس در لمع ییاپ ارک ( و ا ن ن رد " یژتار سا " لماع یع و : ینعی قیقحت یا نمشوه یس یاه یجور
هناریگ یپ
ی ور و یدورو ریداقم ،ینابز یاه ری تم " درجورب یجا ن یاه هنا راک رد هناری شیپ نمشوه یس رد دوجوم اس ی افری 0.8859 اقی د ینعی شاب ) و یو ع عبات PM-DM-SD-ANFIS Rule219 2 1.94

- اشوپ و ی اسن عنص رد وه یشزومآ یاه هداد،یزاف 5 دوجو لع هب PM.DM-SD-ANFIS نمشوه یس PM-DM-SD-ANFIS عبات یرت اب ( و لاماک ی یک ن رد " " لماع یع و و 0.06 ÷ 4=0.015
متسیس یرادهگن هزوح رد لاعف ناگر و ساتید . ادرپ اگر تار ن ی نایم اب
در ورب ی اسن تاجنا راک یو ع عباوت زینو،یعون م اشوپ و ی اسن عیانص رد هناریگشیپ تاریمعت و اب ربارب 243 سا . ؛ نراد 3 ا ا ک ره هک یل ا ری م د ع ی هب لی ت ار ی اف یجور 0.9999 اقی د ینعی شاب ) یو ع 2 1.39
ی ل م دادعا ه ون ا تنا و ین مه و در ورب ی اسن تاجنا راک - اس ی افری م رد یامنیم یع اسا رب اگر تار ن و سا ید هک ییا نآ ا Rule224 0.061 ÷ 4=0.01525
یا رد ی ت رو ب هک یرتکد نایوجشناد یس و ام نمشوه عاو یا ها یاپ هب وبرم ل ش عبات ی اب ارک ن رد " و ( راک یحم " لماع یع و و
یاهری تم اب ترم یا هقنو و یرادرب هرهب ،دنیامنیم یقحت و هع ا م اههزوح نمشوه شور ا MATLAB رن را فا 0.9350 یجور ری م ش ج ون ا نا و یو ع عباوت
نا
متسیس ی ور و یدورو دوش . Wtaver ییاد ی اف شور ه ییا نآ ا ددر یم یرادرب هر ب wtavarr شاب اقی د ینعی شاب ) و یو ع ه ش ایب 5 MF ) ( یاراد Rule235 2 1.78 0.33 ÷ 4=0.0825
ین و هی وا م هب هجوتاب ی - نورد ار یقحت دنمشوه PM.DM-SD-ANFIS
ر ن و سا ید امعا X1 ن رد انکراک لماع : سا لی رش هب شهاک هب اس ی اف ری یا اری ) Then ها نآ ( لا ا رد ا او یم اب رف دوم آ ج ا
یعونصم شوه X2 ن رد یرو نف لماع یاهری تم یارب ییات هس یاه یع د ع ی و ی اف د ع ی یب یر انت یارب ر مک ام ین و ه م یگ ی یپ " : ینعی قیقحت یا نمشوه یس یا یجور یب
م اونع هب آ یبای را ج اگر X3. ن رد یژتار سا لماع ری تم یارب ییات یدورو و 5 . یامنیم مک تا ساحم دو س یم نپ رد ( Y ) " هناری شیپ تاریمعت و یرا ن در لمع ینعی قیقحت یجور ری م یع و PM-DM-SD-ANFIS
.882
( 88%

)
اب ربارب و دراد رار
MF5=V.H
و یلی ینعی
(
اسارب ه عبات ی نی ب
ش ه ی گرب یجور و یدورو اوت یم X4 ن رد ی یک لماع یم هتشا گ یامن هب ؛ی ور اهنآ یبایزرا و یگر دعاو ار تسا لماش یامنیم دا یا یع دا عا ا یا عوم م ای ) سا . درجورب یجا ن تا نا راک رد هناری شیپ تاریمعت و یرا ن
ا نا ار نمشوه یس دعاو هاگیاپ داجیا و ناگر و ساتید سوت ( ی یمها یع و اسا رب PM.DM-SD-ANFIS رد یجور ری م نمشوه لیلحت یارب ؛ قیق رد اگر تار ن ی نایم اب

X5 ن رد راک یحم لماع دوش هب ا ی ری ی اف دا عا ا ی رب ل ا
)
درک یا هعومجم دنمشوه دعاو هاگیاپ . دشا یم دنمشوه ؛یدورو ری م نپ اسا رب یناب و ید ع ترو هب قیقحت یارجا ا پ
دعاو زا نمشوه و یاراد و 0.744 رد ن ؛ اب یر یایوپ و وم ربارب اب انکراک لماع ننو ماک ا : دومن هدا سا لی رش هب
دنمشوه متسیس ل هک سا " رگا - هاگنآ " ا یا رد ندر یم یع د ع ی 0.9129 ا ؛درادن دو و ر ص رف ری پ یارب یفاک لع هک ییاجنآزا
PM.DM-SD-ANFIS ؛ وم آ یا هداد یا ی نایم نمشوه 0.753 لماع یرو نف رد ن ؛ اب یر یایوپ و وم ربارب اب ننو ماک
و یاراد و

ددرگیم وسحم دوشیم هداد سد ا تاعلاطا ا یمک یلی نمشوه یس ا ن سا روتوم رد 0.9239 و ناگر تار ن یگنایم یب ینعی ددرگیم هتفری پ لباقم رف
رد ن ؛ اب یر یایوپ و وم ربارب اب
لماع
PM.DM-SD-ANFIS نمشوه و یاراد و 0.722 یژتار سا ننو ماک
یا یریگ ه ی ن رد اصقن دا یا س ی و " ؛ هناری شیپ تاریمعت و یرا ن ج " 0.8859 ( H0 ) : ر رف ( H1 ) : ر رف یاه"تسیس
(
یمصت ل ا م رد ا وص ددر یمن ییا ن ا ر مک 1 رد ) 0.0085 اب ربارب نمشوه و یاراد و 0.815 0.9999 لماع ی یک رد ن ؛ اب یر یایوپ و وم ربارب اب ننو ماک اب اگر تار ن ی نایم یب اب اگر تار ن ی نایم یب دنمشوه م ی ور
یاهری تم یب لت م یاهت اح و و لامتحا رای ب د هک سا ه ش ه ساحم 0 .762 یاه یجور یاه یجور
هتفرگ ر ن رد ناسکی دنمشوه متسیس یلصا و ینیب شیپ ل ا م یصص ت یریگ یاه ی صع یاه ه ش تا ساحم ی اب نمشوه و یاراد و 0.9350 لماع یحم راک رد ن ؛ اب یر یایوپ و وم ربارب اب ننو ماک نمشوه یس نمشوه یس PM-DM-SD-ANFIS

هاگیاپ ی اس ورش ی . ه قن سا هدش ی اف ق نم و یعونصم هر ب یرادرب ه ش سا 0.935,0.999,0.8859,0.9239,0.9129 اب رو سد
لدم ی رد دعاو رب ینت م یشناد ل مدی وت . سا یرور وص یا رد هری . . ه یم اشن ار قیقحت ( پ ا یارجا قیقحت ورد ی یط شش ییات ؛ شا یم ینعی یع و ی یمها 5.29 آ یجور هک درادن دو و یرادانعم توا ت
یاه ومجم ندروآ سد هب ؛ دنمشوه یایوپ .882 ( .88% اب ربارب و دراد رار ) MF5=V.H( ؛هناری شیپ تاریمعت و یرا ن ) PM-DM-SD-ANFIS PM-DM-SD-ANFIS
رد یع و یلی و

دارفا ناد زا یزاف هاگنآ رگا دعاو زا ه عبات ) سا . درجورب یجا ن تا ن ا راک رد هناری شیپ تاریمعت و یرا ن اسارب ه عبات ی نی ب رب PM.DM-SD-ANFIS رد یجور ری م نمشوه لیلحت یرادانعم توا ت یرادانعم توا ت
PM.DM-SD-ANFIS
:
سا لی رش هب قیقحت هنی ب
؛ دشا یم یسررب دروم هزوح ناد ای هر Y=[0.9129X1+0.9239X2+0.8859X3+0.9999X4+0.935X5]=0.882 نپ اسا رب یناب و ید ع ترو هب ) قیقحت یارجا ا پ ( ی یمها یع و اسا دراد دوجو درا ن دوجو
یدورو ری م