Page 8 - Grafentheorie HS 4 Hamiltongrafen

Grafentheorie

Merk op dat deze voorwaarde VOLDOENDE is maar NIET NOODZAKELIJK.
Er kunnen gemakkelijk tegenvoorbeelden gevonden worden van grafen dit niet volledig zijn maar toch
een Hamiltongraaf.

Criterium 2:
Stelling van Ore (voldoende voorwaarde)

Indien voor een graaf met n knopen (n ≥ 3) voor elk paar niet aangrenzende knopen A en B geldt dat de
som van de graden van deze knopen deg(A) + deg(B) ≥ n, dan is dit een Hamiltongraaf.

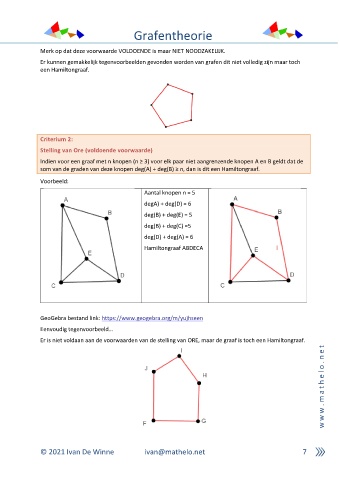
Voorbeeld:

Aantal knopen n = 5
degA) + deg(D) = 6
deg(B) + deg(E) = 5

deg(B) + deg(C) =5
deg(D) + deg(A) = 6

Hamiltongraaf ABDECA

GeoGebra bestand link: https://www.geogebra.org/m/yujhseen

Eenvoudig tegenvoorbeeld…
Er is niet voldaan aan de voorwaarden van de stelling van ORE, maar de graaf is toch een Hamiltongraaf.

t
e
n
.
o
l
e
h
t
a
m
.
w
w
w

© 2021 Ivan De Winne ivan@mathelo.net 7