Page 17 - Grafentheorie HS 3 Graafkleuringen

HS 3 Graafkleuringen

OEFENINGEN hoofdstuk 3: Kleuren van grafen

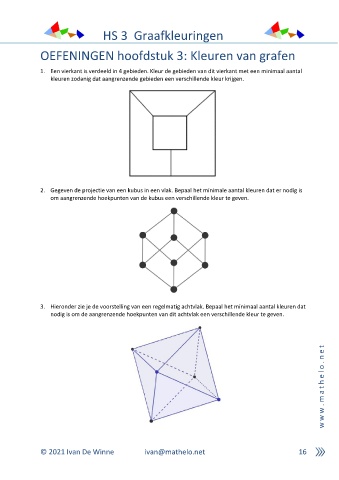
1. Een vierkant is verdeeld in 4 gebieden. Kleur de gebieden van dit vierkant met een minimaal aantal
kleuren zodanig dat aangrenzende gebieden een verschillende kleur krijgen.

2. Gegeven de projectie van een kubus in een vlak. Bepaal het minimale aantal kleuren dat er nodig is
om aangrenzende hoekpunten van de kubus een verschillende kleur te geven.

3. Hieronder zie je de voorstelling van een regelmatig achtvlak. Bepaal het minimaal aantal kleuren dat
nodig is om de aangrenzende hoekpunten van dit achtvlak een verschillende kleur te geven.

t
e
n
.
o
l
e
h
t
a
m
.
w
w
w

© 2021 Ivan De Winne ivan@mathelo.net 16