Page 9 - Grafentheorie HS 3 Graafkleuringen

HS 3 Graafkleuringen

3.4 Planaire grafen

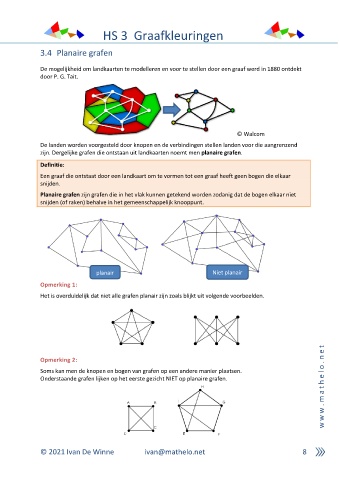
De mogelijkheid om landkaarten te modelleren en voor te stellen door een graaf werd in 1880 ontdekt
door P. G. Tait.

© Walcom
De landen worden voorgesteld door knopen en de verbindingen stellen landen voor die aangrenzend
zijn. Dergelijke grafen die ontstaan uit landkaarten noemt men planaire grafen.

Definitie:
Een graaf die ontstaat door een landkaart om te vormen tot een graaf heeft geen bogen die elkaar
snijden.
Planaire grafen zijn grafen die in het vlak kunnen getekend worden zodanig dat de bogen elkaar niet
snijden (of raken) behalve in het gemeenschappelijk knooppunt.

planair Niet planair
Opmerking 1:
Het is overduidelijk dat niet alle grafen planair zijn zoals blijkt uit volgende voorbeelden.

t
e
Opmerking 2: n
.
o
Soms kan men de knopen en bogen van grafen op een andere manier plaatsen. l
Onderstaande grafen lijken op het eerste gezicht NIET op planaire grafen. e
h
t
a
m
.
w
w
w

© 2021 Ivan De Winne ivan@mathelo.net 8