Page 204 - Geogebra 6 van A tot Z
P. 204
GeoGebra 6 van A tot Z
10.9 Analyse
10.9.1 Limieten en asymptoten
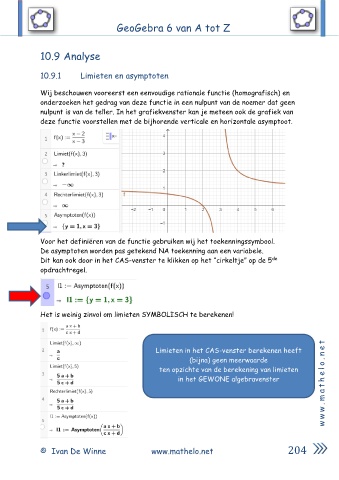
Wij beschouwen vooreerst een eenvoudige rationale functie (homografisch) en
onderzoeken het gedrag van deze functie in een nulpunt van de noemer dat geen
nulpunt is van de teller. In het grafiekvenster kan je meteen ook de grafiek van
deze functie voorstellen met de bijhorende verticale en horizontale asymptoot.
Voor het definiëren van de functie gebruiken wij het toekenningssymbool.
De asymptoten worden pas getekend NA toekenning aan een variabele.
de
Dit kan ook door in het CAS-venster te klikken op het “cirkeltje” op de 5
opdrachtregel.
Het is weinig zinvol om limieten SYMBOLISCH te berekenen!
t
Limieten in het CAS-venster berekenen heeft e
(bijna) geen meerwaarde n .
ten opzichte van de berekening van limieten o l
in het GEWONE algebravenster e h
t
a
m
.
w
w
w
© Ivan De Winne www.mathelo.net 204