Page 212 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

In dit geval moet men wel de vergelijkingen en de namen van de onbekenden a, b, c
ingeven als een lijsten. Met het $-teken kun je eenvoudig verwijzen naar de output
van de verschillende commandoregels.

Door gebruik te maken van de commando’s Element( ) en Rechterlid( ) kan je de
bijhorende grafiek laten tekenen.

Voorbeeld 2

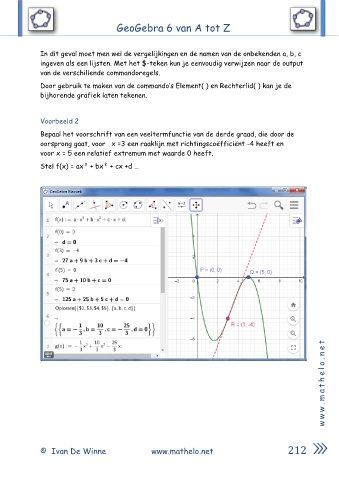
Bepaal het voorschrift van een veeltermfunctie van de derde graad, die door de
oorsprong gaat, voor x =3 een raaklijn met richtingscoëfficiënt -4 heeft en
voor x = 5 een relatief extremum met waarde 0 heeft.

Stel f(x) = ax³ + bx² + cx +d …

t
e
n
.
o
l
e
h
t
a m
. w

w
w

© Ivan De Winne www.mathelo.net 212