Page 14 - HS 3 Graspable Math

Graspable Math

3.6.5 Stelsel vergelijkingen van de eerste graad oplossen.

Bij het oplossen van een stelsel van vergelijkingen van de eerste graad zijn er verschillende
methoden; door gelijkstelling, door combinatie of substitutie.

Je kan bij het oplossen van zo’n stelsel ook de grafische voorstelling maken met GeoGebra.
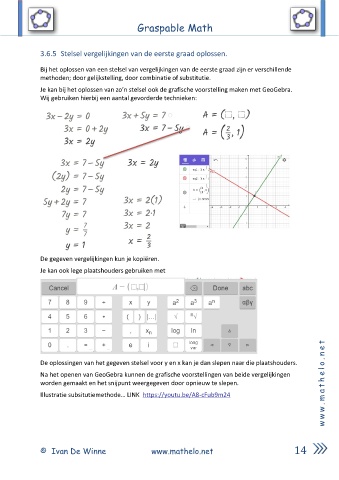
Wij gebruiken hierbij een aantal gevorderde technieken:

De gegeven vergelijkingen kun je kopiëren.

Je kan ook lege plaatshouders gebruiken met

t
e
n
.
De oplossingen van het gegeven stelsel voor y en x kan je dan slepen naar die plaatshouders. o
l
Na het openen van GeoGebra kunnen de grafische voorstellingen van beide vergelijkingen e
worden gemaakt en het snijpunt weergegeven door opnieuw te slepen. h
t
a
Illustratie subsitutiemethode… LINK https://youtu.be/A8-cFub9m24
m
.
w
w
w

© Ivan De Winne www.mathelo.net 14