Page 8 - libro digital F

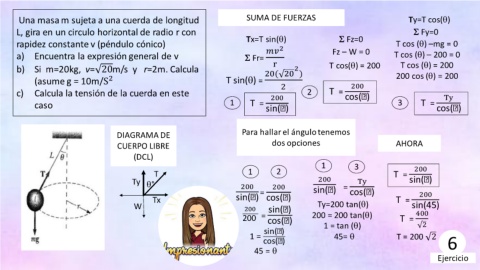
Una masa m sujeta a una cuerda de longitud SUMA DE FUERZAS Ty=T cos()

L, gira en un circulo horizontal de radio r con  Fy=0
Tx=T sin()  Fz=0
rapidez constante v (péndulo cónico) T cos () –mg = 0
2 Fz – W = 0
a) Encuentra la expresión general de v  Fr= T cos () – 200 = 0
r T cos() = 200 T cos () = 200
b) Si m=20kg, v= 20m/s y r=2m. Calcula

(asume g = 10m/S 2 T sin() = 200 200 cos () = 200

c) Calcula la tensión de la cuerda en este 200 2 T = cos( ) Ty

caso 1 T = sin( ) 3 T = cos( )

DIAGRAMA DE Para hallar el ángulo tenemos

CUERPO LIBRE dos opciones AHORA
(DCL)
1 3 200
T 1 2 T =
200
Ty ° 200 200 sin( ) = Ty sin( )

Tx sin( ) = cos( ) cos( ) T = 200
W 200 sin( ) Ty=200 tan() sin(45)

200 = cos( ) 200 = 200 tan() T = 400

sin( ) 1 = tan () 2
1 = 45=  T = 200 2
cos( ) 6
45 = 

Ejercicio