Page 10 - (1-1)_Neat
P. 10
A1 ) ١ – ١ ( ىﺮﻤﻋ ﻦﻣ تﺎـﻓ ﻰﻠﻟا
ةيعيبرتلا ةلادلا
.ﺮفص ، ا \ + س ب + ٢ س ا = ( س د ) وه ةي عيبﺮتلا ةلادل ل ةﻣاعلا ةروصلا
ك ٢ – ه ( + س ا ) = ( س ) د لكشلا ىلع اهتباتك نكمي ةروصلا هذه
ه ( ، ) د = ك ، ب = ه ثيح ( ك ه ، ) هسأر ئفاكﻣ عطق وه اهل ىنايبلا مسﺮلا
ا 2
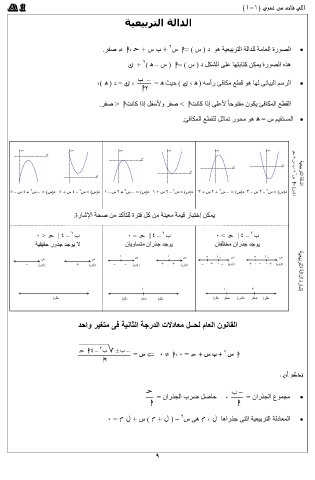
.ﺮفص > ا ﺖناك اذإ لفسﻷو ﺮفص < ا ﺖناك اذإ ىلعﻷ ً ا حوتفﻣ نوكي ئفاكملا عطقلا
. ئفاكملا عطقلل لثامت روحﻣ وه ه = س ميقتسملا
ص ص ص ص ص ص
س \
س +
س س س س ب +
س س ةيعيبﺮتلا ةلادلا
٢
ا
=
– ٥ س + ٤ ٢ س – = (س)د + ٥ س – ٤ ٢ س = (س)د – ١ س + ٢ ٢ س – = (س)د + ١ س – ٢ ٢ س = (س)د + ٣ س ٢ + ٢ س – = (س)د – ٣ س – ٢ ٢ س = (س)د (س)د
.ةراشﻹا ةحص نﻣ دكأتلل ةﺮتف لك نﻣ ةنيعﻣ ةميق رابتخإ نكمي
– ٤ ا
٠ > \ – ٤ ا ٢ ب ٠ = \ ٢ ب ٠ < \ – ٤ ا ٢ ب
ةيقيقح روذج دجوي ﻻ نايواستﻣ نارذج دجوي نافلتﺨﻣ نارذج د جوي
١ ١ – ١ س – ١ س
س س س س ٣ ٣
– (س)د + (س)د (س)د + + (س)د ٠ + ٠ (س)د + ٠ – ٠ + (س)د
١ - ١ ٣
ةيعيبﺮتلا ةلادلا ةراشإ
ا لثﻣ ا لثﻣ ﺮفص ا لثﻣ ا لثﻣ ﺮفص ا سكع ﺮفص ا لثﻣ
دحاو ريغتم ىف ةيناثلا ةجردلا تﻻداعم لــح ل ماعلا نوناقلا
\ ا 4 2 بØ ب ٢
= س ٠ ، ا ٠ = \ + س ب + س ا
2 ا
: نأ ﺮﻛﺬﺗ
\ ب
= نارذجلا بﺮض لصاح ، = نارذجلا عومجﻣ
ا ا
٠ = ل م + س ( م + ل – ) ٢ س ىه م ل ، اهارذج ىتلا ةيعيبﺮتلا ةلداعملا
٩