Page 23 - (1-1)_Neat

ﻰﻟوﻷا ﺔﻘﺘﺸﻤﻟا ) ١ – ١ (

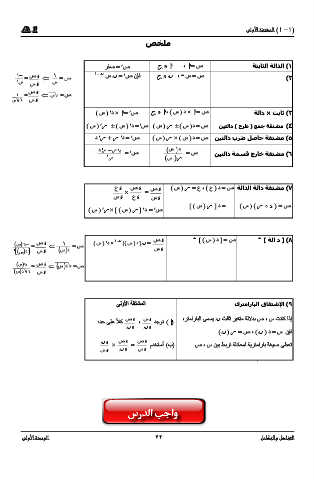
ﺺﺨﻠم

رﻔﺻ =  ص á ا  ا ، = ص ةتباثلا ةلادلا ( ١
1  = ص ء  1 = ص – ١ ن س ن =  ص نإف á  ن ، ن س = ص ( ٢
2 س س ء س

1 = ص ء  سØ = ص
Ø
س 2 س ء
( س د  ) × ا =  ص á ا  ، ( س د ) × ا = ص ةلاد × ﺖباﺛ ( ٣
( س )  ر  ( س )  د =  ص ( س ) ر  ( س ) د = ص نيتلاد ( حرط ) ع مج ةقتشم ( ٤

 د ر + ر  د =  ص ( س ) ر × ( س ) د = ص نيتلاد برض لصاح ةقتشم ( ٥
د '  ر  س  د
ر
'د =  ص = ص نيتلاد ةمسق جراخ ةقتشم ( ٦

2 ر  س ر

ع ء صء ص ء ( س ) ر = ع ، ( ) ع د = ص ةلادلا ةلاد ةقتشم ( ٧
 =
س ء عء س ء

( س )  ر × [ ( س ) ر د  ] =  ص [ ( س ) ر ] د = ( س ) ( ر  د ) = ص

س
  د  = ص ء  1 = ص ( س × د  ) - ١ ن ( [ س ن ] د ) = ص ء ن [ ( س د ) ] = ص ن [ ةلا د ] ( ٨
س ء
س
2   د  س ء  د
س
 
س
  د = ص ء   د Ø = ص
س
 د Ø 2 س ء
س

ىلوﻷا ةقتشملا ى رتمارابلا قا قتشﻹا ( ٩
ص ء س ء ،رﺘمارابلا ىمسي ن ثلاث ريغﺘم ةلﻻدب ص ، س تناك اذإ
هدح ىلع ًﻼك ، دجون ) ا (
نء نء
( ن ) ر = ص ، ( ن ) د = س نإف
ن ء ص ء ص ء
× = مدخﺘسأ (ب) ص ، س نيب طبرت ةلداعمل ةيرﺘماراب ةغيﺻ ىطعت
س ء نء س ء

ﻰﻟوﻷا ةﺪﺣﻮﻟا ٢٢ ﻞﻣﺎﻜﺘﻟاو ﻞﺿﺎـﻔﺘﻟا