Page 54 - E-MODUL TRANSFORMASI GEOMETRI BERBANTU APLIKASI GEOGEBRA KELAS IX SMP

Contoh 3 : Dilatasi bangun segi empat dengan pusat dilatasi di titik P

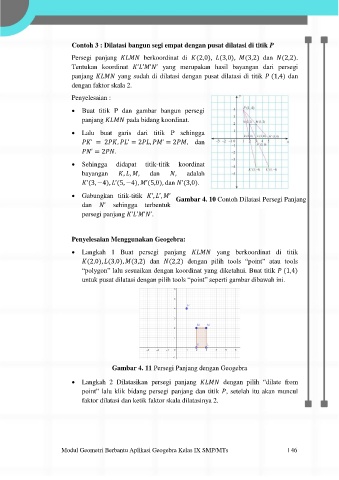
Persegi panjang berkoordinat di (2,0), (3,0), (3,2) dan (2,2).
Tentukan koordinat ’ ’ ’ ’ yang merupakan hasil bayangan dari persegi
panjang yang sudah di dilatasi dengan pusat dilatasi di titik (1,4) dan
dengan faktor skala 2.

Penyelesaian :
 Buat titik P dan gambar bangun persegi
panjang pada bidang koordinat.

 Lalu buat garis dari titik P sehingga
’ = 2 , ’ = 2 , ’ = 2 , dan
’ = 2 .

 Sehingga didapat titik-titik koordinat
bayangan , , , dan , adalah
’(3, −4), ’(5, −4), ’(5,0), dan ’(3,0).

 Gabungkan titik-titik ’, ’, ’ Gambar 4. 10 Contoh Dilatasi Persegi Panjang
dan ’ sehingga terbentuk
persegi panjang ’ ’ ’ ’.

Penyelesaian Menggunakan Geogebra:
 Langkah 1 Buat persegi panjang yang berkoordinat di titik
(2,0), (3,0), (3,2) dan (2,2) dengan pilih tools “point” atau tools
“polygon” lalu sesuaikan dengan koordinat yang diketahui. Buat titik (1,4)
untuk pusat dilatasi dengan pilih tools “point” seperti gambar dibawah ini.

Gambar 4. 11 Persegi Panjang dengan Geogebra

 Langkah 2 Dilatasikan persegi panjang dengan pilih “dilate from
point” lalu klik bidang persegi panjang dan titik , setelah itu akan muncul
faktor dilatasi dan ketik faktor skala dilatasinya 2.

Modul Geometri Berbantu Aplikasi Geogebra Kelas IX SMP/MTs | 46