Page 8 - E-Book_Ni Kadek Sintya Dewi_Turunan Fungsi Aljabar

Misalkan seseorang yang sedang bermain papan seluncur bergerak dari titik ( , )
2
2
dan melayang ke udara pada titik ( , ) sehingga ia bergerak dari titik mendekati
1
1
titik P. Garis yang menghubungkan titik ( , ) dan titik ( , ) disebut tali busur
1
2
2
1
atau garis sekan dengan kemiringan atau gradien = 2 − 1 (Ingat konsep garis lurus)
2 − 1
Jika ∆ = − maka = ∆ + (∆ merupakan selisih dari x) dan jika ∆ =
2
2
1
1
− maka = ∆ −
1
2
1
2
Jika ∆ semakin kecil maka akan bergerak mendekati P (Jika ∆ → 0 maka → ).
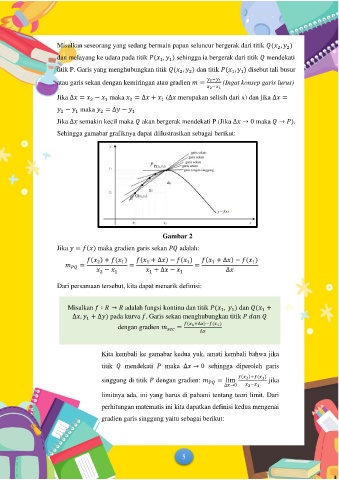
Sehingga gamabar grafiknya dapat diilustrasikan sebagai berikut:

Gambar 2

Jika = ( ) maka gradien garis sekan adalah:
( ) + ( ) ( + ∆ ) − ( ) ( + ∆ ) − ( )
1
1
2
1
1
1
= = =
− 1 + ∆ − 1 ∆
1
2
Dari persamaan tersebut, kita dapat menarik definisi:

Misalkan ∶ → adalah fungsi kontinu dan titik ( , ) dan ( +
1
1
1
∆ , + ∆ ) pada kurva . Garis sekan menghubungkan titik
1
( 1 +∆ )− ( 1 )
dengan gradien =
∆

Kita kembali ke gamabar kedua yuk, amati kembali bahwa jika
titik mendekati maka ∆ → 0 sehingga diperoleh garis

singgung di titik dengan gradien: = lim ( 2 )+ ( 1 ) jika
∆ →0 2 − 1
limitnya ada, ini yang harus di pahami tentang teori limit. Dari
perhitungan matematis ini kita dapatkan definisi kedua mengenai

gradien garis singgung yaitu sebagai berikut:

5