Page 15 - Производная_Финал

При ∆x → 0 имеем также ∆v → 0, поэтому

u(v(x) + ∆v) − u(v(x))
0
→ u (v(x)).
∆v
Следовательно,
u(v(x) + ∆v) − u(v(x)) ∆v
0
0
0
f (x) = lim = u (v(x))v (x),
∆x→0 ∆v ∆x

что и требовалось. Для более полного ознакомления см.здесь.

1.8 Геометрический смысл производной

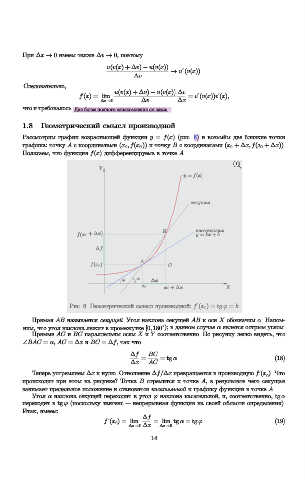
Рассмотрим график возрастающей функции y = f(x) (рис. 6) и возьмём две близкие точки

графика: точку A с координатами (x 0 , f(x 0 )) и точку B с координатами (x 0 + ∆x, f(x 0 + ∆x)).

Полагаем, что функция f(x) дифференцируема в точке A.
Y
y = f(x)
секущая
B касательная
f(x 0 + ∆x) y = kx + b
∆f
A
f(x 0 ) C
ϕ α ∆x
x 0 x 0 + ∆x X
0
Рис. 6. Геометрический смысл производной: f (x 0 ) = tg ϕ = k
Прямая AB называется секущей. Угол наклона секущей AB к оси X обозначим α. Напом-
◦
ним, что угол наклона лежит в промежутке [0, 180 ); в данном случае α явлется острым углом.
Прямые AC и BC параллельны осям X и Y соответственно. По рисунку легко видеть, что
∠BAC = α, AC = ∆x и BC = ∆f, так что
∆f BC
= = tg α. (18)
∆x AC
0
Теперь устремляем ∆x к нулю. Отношение ∆f/∆x превращается в производную f (x 0 ). Что
происходит при этом на рисунке? Точка B стремится к точке A, в результате чего секущая
занимает предельное положение и становится касательной к графику функции в точке A.
Угол α наклона секущей переходит в угол ϕ наклона касательной, и, соответственно, tg α
переходит в tg ϕ (поскольку тангенс непрерывная функция на своей области определения).
Итак, имеем:
∆f
0
f (x 0 ) = lim = lim tg α = tg ϕ. (19)
∆x→0 ∆x ∆x→0
14