Page 20 - 책(종합)

개 념 04 여집합과 차집합

. 1 여집합
) 1 여집합
U
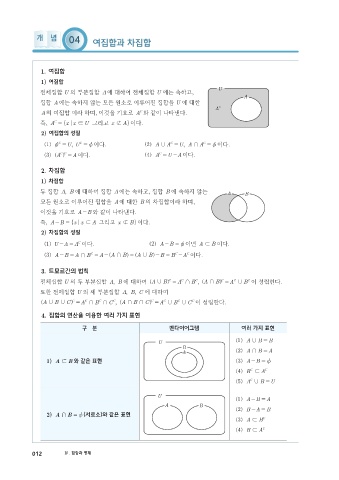
전체집합 U 의 부분집합 A 에 대하여 전체집합 U 에는 속하고,
A
집합 A 에는 속하지 않는 모든 원소로 이루어진 집합을 U 에 대한
A C
C
A 의 여집합 이라 하며, 이것을 기호로 A 와 같이 나타낸다.
x
C
즉, A = {| x ! U 그리고 x g A }이다.
) 2 여집합의 성질
C
1 ]g z = , UU = z 이다. 2 ]g A , A = , UA + A = z 이다.
C
C
C
3 ]g A C C = A 이다. 4 ]g A = U - 이다.
C
A
]g
2. 차집합
) 1 차집합
두 집합 ,AB 에 대하여 집합 A 에는 속하고, 집합 B 에 속하지 않는 A B
모든 원소로 이루어진 집합을 A 에 대한 B 의 차집합이라 하며,
이것을 기호로 A - B 와 같이 나타낸다.
즉, A - B = {|xx ! A 그리고 x g B }이다.
) 2 차집합의 성질

C
1 ]g U - A = A 이다. 2 ]g A - B = z 이면 A 1 B 이다.
C
C
C
3 ]g A - B = A + B = A - ] A + g A , g B = B - A 이다.
B -
B = ]
3. 드모르간의 법칙
C
B =
C
C
B =
전체집합 U 의 두 부분집합 ,AB 에 대하여 A , g C A + B C , A + g C A , B 이 성립한다.
]
]
,
또한 전체집합 U 의 세 부분집합 ,AB C 에 대하여
C
C
C
C =
C
C
C =
]
] A , B , g C A + B + C C , A + B + g C A , B , C 이 성립한다.
4. 집합의 연산을 이용한 여러 가지 표현
구 분 벤다이어그램 여러 가지 표현
1 ]g A , B = B
U
B 2 ]g A +
A B = A
) 1 A 1 B 와 같은 표현 3 ]g A - B = z
C
4 ]g B 1 A C
5 ]g A , B = U
C
U
1 ]g A - B = A
A B
2 ]g B - A = B
) 2 A + B = z (서로소)와 같은 표현
3 ]g A 1 B C
4 ]g B 1 A C
012 Ⅳ. 집합과 명제