Page 107 - 책(종합)

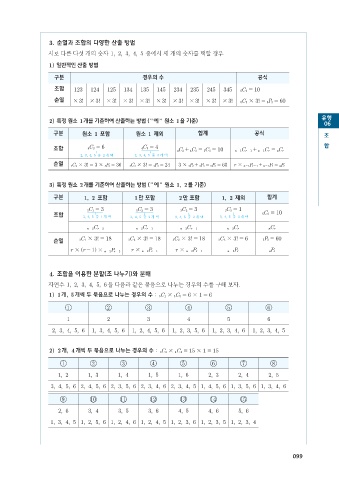
3. 순열과 조합의 다양한 산출 방법
,
,
,
서로 다른 다섯 개의 숫자 ,12 34 5 중에서 세 개의 숫자를 택할 경우
) 1 일반적인 산출 방법
구분 경우의 수 공식

조합 123 124 125 134 135 145 234 235 245 345 5 C 3 = 10
순열 # ! 3 # ! 3 # ! 3 # ! 3 # ! 3 # ! 3 # ! 3 # ! 3 # ! 3 # ! 3 5 C 3 # ! 3 = 5 P 3 = 60

유형
) 2 특정 원소 1개를 기준하여 산출하는 방법 (^예_ 원소 1을 기준) 06

구분 원소 1 포함 원소 1 제외 합계 공식 조

4
6
조합 4 C 2 = 4 C 3 = 4 C 2 + 4 C 3 = 5 C 3 = 10 n- 1 C r- 1 + n- 1 C r = n C r 합
,
,
,
,
, 23 45 중 2 개 택 , 23 45 중 3 개 택
순열 4 C 2 # ! 3 = 3 # 4 P 2 = 36 4 C 3 # ! 3 = 4 P 3 = 24 3 # 4 P 2 + 4 P 3 = 5 P 3 = 60 r # n- 1 P r- 1 + n- 1 P r = n P r
3) 특정 원소 2개를 기준하여 산출하는 방법 (^예_ 원소 ,12를 기준)
구분 , 12 포함 1 만 포함 2 만 포함 , 12 제외 합계
C 1 = 3 C 2 = 3 C 2 = 3 C 3 = 1
3 3 3 3 C 3 = 10
조합 , 34 5 중 1 개 택 , 34 5 중 2 개 택 , 34 5 중 2 개 택 , 34 5 중 3 개 택 5
,
,
,
,
n- 2 C r- 2 n- 2 C r- 1 n- 2 C r- 1 n- 2 C r n C r
C 1 # ! 3 = 18 C 2 # ! 3 = 18 C 2 # ! 3 = 18 C 3 # ! 3 = 6 P 3 = 60
순열 3 3 3 3 5
1 #
r # ] r - g n- 2 P r- 2 r # n- 2 P r- 1 r # n- 2 P r- 1 n- 2 P r n P r

4. 조합을 이용한 분할(조 나누기)와 분배

,
,
,
,
자연수 ,12 34 56을 다음과 같은 묶음으로 나누는 경우의 수를 구해 보자.
) 1 1 개, 5 개씩 두 묶음으로 나누는 경우의 수 : C 1 # 5 C 5 = 6 # 1 =
6
6
1 2 3 4 5 6
1 2 3 4 5 6
,
,
,
,
,
,
,
,
,
,
,
, 23 45 6 , 13 45 6 , 12 45 6 , 1235 6 , 12 34 6 , 12 34 5
,
,
,
,
,
,
,
) 2 2 개, 4 개씩 두 묶음으로 나누는 경우의 수 : C 2 # 4 C 4 = 15 # 1 = 15
6
1 2 3 4 5 6 7 8
, 12 , 13 , 14 , 15 , 16 , 23 , 24 , 25
,
,
, 34 56 24 56 2356 23 46 23 45 14 56 1356 13 46
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
9 10 11 12 13 14 15
, 26 , 34 , 35 , 36 , 45 , 46 , 56
,
,
,
,
,
,
,
,
,
, 13 45 1256 12 46 12 45 1236 1235 12 34
,
,
,
,
,
,
,
,
,
,
,
099