Page 57 - 책(종합)

알맹이 콕 !

. 1 대응과 함수
) 1 대응
,
,
,
,
오른쪽 그림은 집합 X = " , 12 34, 의 각 원소에 집합 Y = " , ab cd, 의 원소를 X Y
1 a
짝지어 놓은 것이다. 이때 1 에는 ,b 2 에는 ,a 3 에는 ,c 4 에는 c 가 대응한다 하며
기호로 1 $ , b 2 $ , a 3 $ , c 4 $ 와 같이 나타낸다. 2 b
c
3 c 유형
또한 집합 X 의 모든 원소는 1 $ , b 2 $ , a 3 $ , c 4 $ 와 같이 03
c
4 d
집합 Y 의 원소에 오직 하나씩 대응할 때, X 에서 Y 로의 함수라 한다.
함
) 2 함수
수
1 ]g X[ 의 각 원소에 \ 라는 뜻은 X[ 의 원소가 하나도 빠지지 않고 모두 \ 라는 뜻이고,
Y[ 의 원소가 오직 하나씩 \ 이라는 뜻은 X[ 의 원소 하나에 Y 의 원소가 두개 이상 대응해서는 안된다. \ 는 뜻이다.
2 ]g 함수가 될 수 없는 경우는 다음과 같다.
① 집합 X 의 원소 중에서 집합 Y 에 대응하지 않고 남아 있는 원소가 있을 때
② 집합 X 의 한 원소에 집합 Y 의 원소가 두 개 이상 대응할 때
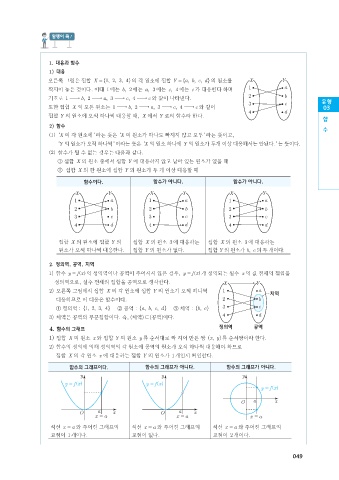
함수이다. 함수가 아니다. 함수가 아니다.

X Y X Y X Y
1 a 1 a 1 a
2 b 2 b 2 b
3 c 3 c 3 c
4 d 4 d 4 d

집합 X 의 원소에 집합 Y 의 집합 X 의 원소 3 에 대응하는 집합 X 의 원소 3 에 대응하는
원소가 오직 하나씩 대응한다. 집합 Y 의 원소가 없다. 집합 Y 의 원소가 ,bc 의 두 개이다.

. 2 정의역, 공역, 치역
f x
f x
) 1 함수 y = ]g 의 정의역이나 공역이 주어지지 않은 경우, y = ]g 가 정의되는 실수 x 의 값 전체의 집합을
정의역으로, 실수 전체의 집합을 공역으로 생각한다. X Y
) 2 오른쪽 그림에서 집합 X 의 각 원소에 집합 Y 의 원소가 오직 하나씩 1 a
치역
대응하므로 이 대응은 함수이다. 2 b
,
,
,
,
,
,
,
"
"
"
① 정의역 : 12 34, ② 공역 : ab cd, ③ 치역 : bc, 3 c
) 3 치역은 공역의 부분집합이다. 즉, (치역)1(공역)이다. 4 d
4. 함수의 그래프 정의역 공역
,
) 1 집합 X 의 원소 x 와 집합 Y 의 원소 y 를 순서대로 짝 지어 만든 쌍 xyh 를 순서쌍이라 한다.
^
) 2 함수의 정의에 의해 정의역의 각 원소에 공역의 원소가 오직 하나씩 대응해야 하므로
집합 X 의 각 원소 x 에 대응하는 집합 Y 의 원소가 1 개인지 확인한다.
함수의 그래프이다. 함수의 그래프가 아니다. 함수의 그래프가 아니다.
y y y
f x
f x
y = ]g y = ]g
f x
y = ]g
O a x
O a x O a x
x = a x = a x = a
직선 x = a 와 주어진 그래프의 직선 x = a 와 주어진 그래프의 직선 x = a 와 주어진 그래프의
교점이 1 개이다. 교점이 없다. 교점이 2 개이다.

049