Page 60 - 수학(하)

개 념 03 합성함수

. 1 합성함수
) 1 gf%

%
,
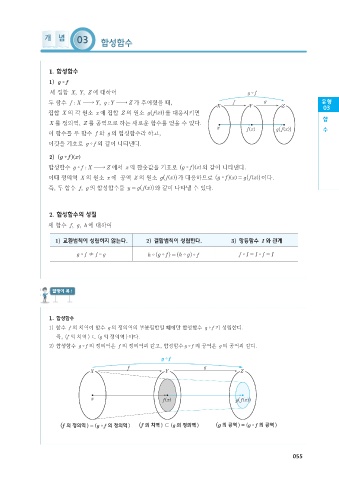
세 집합 ,XY Z 에 대하여 gf
두 함수 fX $ , Yg Y $ Z 가 주어졌을 때, f g 유형
:
:
X Y Z 03
^
집합 X 의 각 원소 x 에 집합 Z 의 원소 g f x ]gh 를 대응시키면
함
X 를 정의역, Z 를 공역으로 하는 새로운 함수를 얻을 수 있다.
x f x ]g g f x ]gh 수
^
이 함수를 두 함수 f 와 g 의 합성함수라 하고,
이것을 기호로 gf% 와 같이 나타낸다.
^
) 2 gf x% h ] g
합성함수 gf X $% : Z 에서 x 의 함숫값을 기호로 gf x% h g 와 같이 나타낸다.
^
]
g f x ] gh 이다.
^
^
]
이때 정의역 X 의 원소 x 에 공역 Z 의 원소 g f x ]gh 가 대응하므로 gf x% h g = ^
g f x
즉, 두 함수 ,fg 의 합성함수를 y = ^ ]gh 와 같이 나타낼 수 있다.
2. 합성함수의 성질
,
세 함수 ,fg h 에 대하여
) 1 교환법칙이 성립하지 않는다. 2) 결합법칙이 성립한다. ) 3 항등함수 I 와 관계

%
%
%
%
gf ! fg h % ^ gf = ^h hg % f fI = If = I
%
% h
알맹이 콕 !

. 1 합성함수
) 1 함수 f 의 치역이 함수 g 의 정의역의 부분집합일 때에만 합성함수 gf% 가 성립한다.
즉, (f 의 치역 ) 1 (g 의 정의역 )이다.
) 2 합성함수 gf% 의 정의역은 f 의 정의역과 같고, 합성함수 gf% 의 공역은 g 의 공역과 같다.

%
gf
f g
X Y Z

x f x ]g g f x ]gh
^

%
%
(f 의 정의역 ) = (gf 의 정의역 ) (f 의 치역 ) 1 (g 의 정의역 ) (g 의 공역 ) = (gf 의 공역 )

055