Page 36 - كورس الهندسة المنسية-Copy.pdf عمر
P. 36
محيط مثلث متساوى الأضلاع طول ضلعه 3سم
المحيط =
المحيط
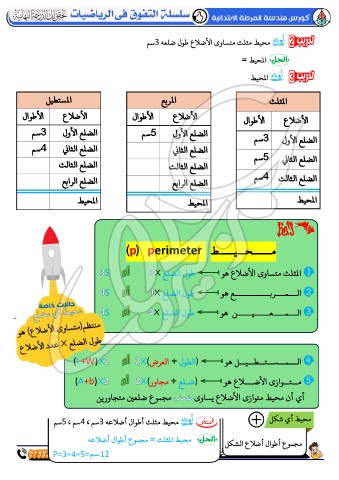
المستطيل المربع المثلث
الأضلاع الأطوال الأضلاع الأطوال
الأطوال الأضلاع
الضلع الأول 3سم الضلع الأول 5سم 3سم الضلع الأول
الضلع الثاني 4سم الضلع الثاني 5سم الضلع الثاني
الضلع الثالث 4سم الضلع الثالث
الضلع الثالث الضلع الرابع
الضلع الرابع المحيط
المحيط
المحيط
مـــــحــيــــط )p( perimeter
محيط أي مضلع 3S المثلث متساوى الأضلاع هو ﻠ طول الضلع ×3
4S الـــمـــربــــــــــــع هو ﻠ طول الضلع ×4
4S الـــمــــعـــــيـــــن هو ﻠ طول الضلع ×4
الـــمــســتــطــيــل هو ﻠ (الطول +العرض)×(L+W)×2 2
مــتــوازى الأضـــلاع هو ﻠ (ضـلع +مجاور)×(A+b)×2 2
أي أن محيط متوازى الأضلاع يساوى ضعف مجموع ضلعين متجاورين
محيط مثلث أطوال أضلاعه 3سم 4 ،سم 5 ،سم محيط أي شكل
محيط المثلث = مجموع أطوال أضلاعه مجموع أطوال أضلاع الشكل
12سم=P=3+4+5 36