Page 259 - Deep Learning

242 Adaptation

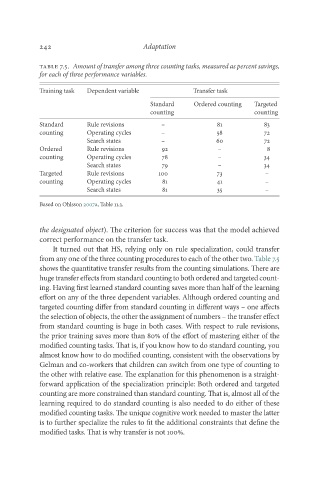
Table 7.5. Amount of transfer among three counting tasks, measured as percent savings,
for each of three performance variables.

Training task Dependent variable Transfer task
Standard Ordered counting Targeted
counting counting
Standard Rule revisions – 81 83
counting Operating cycles – 58 72
Search states – 60 72
Ordered Rule revisions 92 – 8
counting Operating cycles 78 – 34
Search states 79 – 34
Targeted Rule revisions 100 73 –
counting Operating cycles 81 41 –
Search states 81 35 –

Based on Ohlsson 2007a, Table 11.3.

the designated object). The criterion for success was that the model achieved
correct performance on the transfer task.
It turned out that HS, relying only on rule specialization, could transfer
from any one of the three counting procedures to each of the other two. Table 7.5
shows the quantitative transfer results from the counting simulations. There are
huge transfer effects from standard counting to both ordered and targeted count-
ing. Having first learned standard counting saves more than half of the learning
effort on any of the three dependent variables. Although ordered counting and
targeted counting differ from standard counting in different ways – one affects
the selection of objects, the other the assignment of numbers – the transfer effect
from standard counting is huge in both cases. With respect to rule revisions,
the prior training saves more than 80% of the effort of mastering either of the
modified counting tasks. That is, if you know how to do standard counting, you
almost know how to do modified counting, consistent with the observations by
Gelman and co-workers that children can switch from one type of counting to
the other with relative ease. The explanation for this phenomenon is a straight-
forward application of the specialization principle: Both ordered and targeted
counting are more constrained than standard counting. That is, almost all of the
learning required to do standard counting is also needed to do either of these
modified counting tasks. The unique cognitive work needed to master the latter
is to further specialize the rules to fit the additional constraints that define the
modified tasks. That is why transfer is not 100%.