Page 45 - Data Science Algorithms in a Week

Naive Bayes

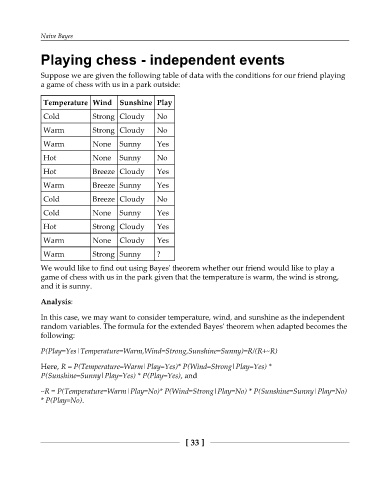
Playing chess - independent events

Suppose we are given the following table of data with the conditions for our friend playing
a game of chess with us in a park outside:

Temperature Wind Sunshine Play
Cold Strong Cloudy No

Warm Strong Cloudy No
Warm None Sunny Yes
Hot None Sunny No

Hot Breeze Cloudy Yes
Warm Breeze Sunny Yes

Cold Breeze Cloudy No
Cold None Sunny Yes
Hot Strong Cloudy Yes

Warm None Cloudy Yes
Warm Strong Sunny ?

We would like to find out using Bayes' theorem whether our friend would like to play a
game of chess with us in the park given that the temperature is warm, the wind is strong,
and it is sunny.
Analysis:

In this case, we may want to consider temperature, wind, and sunshine as the independent
random variables. The formula for the extended Bayes' theorem when adapted becomes the
following:

P(Play=Yes|Temperature=Warm,Wind=Strong,Sunshine=Sunny)=R/(R+~R)

Here, R = P(Temperature=Warm|Play=Yes)* P(Wind=Strong|Play=Yes) *
P(Sunshine=Sunny|Play=Yes) * P(Play=Yes), and

~R = P(Temperature=Warm|Play=No)* P(Wind=Strong|Play=No) * P(Sunshine=Sunny|Play=No)
* P(Play=No).

[ 33 ]