Page 328 - Fingerprints of the Gods by Graham Hancock

Graham Hancock – FINGERPRINTS OF THE GODS

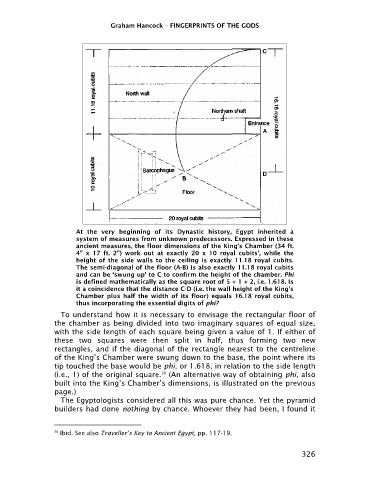
At the very beginning of its Dynastic history, Egypt inherited a
system of measures from unknown predecessors. Expressed in these
ancient measures, the floor dimensions of the King’s Chamber (34 ft.
4” x 17 ft. 2”) work out at exactly 20 x 10 royal cubits’, while the
height of the side walls to the ceiling is exactly 11.18 royal cubits.
The semi-diagonal of the floor (A-B) is also exactly 11.18 royal cubits
and can be ‘swung up’ to C to confirm the height of the chamber. Phi
is defined mathematically as the square root of 5 + 1 + 2, i.e. 1.618. Is
it a coincidence that the distance C-D (i.e. the wall height of the King’s
Chamber plus half the width of its floor) equals 16.18 royal cubits,
thus incorporating the essential digits of phi?
To understand how it is necessary to envisage the rectangular floor of
the chamber as being divided into two imaginary squares of equal size,
with the side length of each square being given a value of 1. If either of
these two squares were then split in half, thus forming two new
rectangles, and if the diagonal of the rectangle nearest to the centreline
of the King’s Chamber were swung down to the base, the point where its
tip touched the base would be phi, or 1.618, in relation to the side length
(i.e., 1) of the original square. (An alternative way of obtaining phi, also
30
built into the King’s Chamber’s dimensions, is illustrated on the previous
page.)
The Egyptologists considered all this was pure chance. Yet the pyramid
builders had done nothing by chance. Whoever they had been, I found it

30 Ibid. See also Traveller’s Key to Ancient Egypt, pp. 117-19.

326